 |
Poisson-Verteilung |
Siméon
Poisson, Mathematiker und Physiker, 26.06.1781 bis 25.04.1840 |
Für kleine Erfolgswahrscheinlichkeiten kann die Binomialverteilung durch die Poisson-Verteilung angenähert werden. D. h., sie gilt, wenn die durchschnittliche Anzahl der Ereignisse das Ergebnis einer sehr großen Zahl von Ereignismöglichkeiten und einer sehr kleinen Ereigniswahrscheinlichkeit ist. | |||
Praktische Beispiele sind: |
| |||||||||||||||
Über die Poisson-Verteilung lässt sich also die Fehlerwahrscheinlichkeit pro Einheit ermitteln. | |||||||||||||||
Wenn, ausgehend von der Binomialverteilung, n sehr groß und p (Erfolgswahrscheinlichkeit) klein ist, dann ist | |||||||||||||||
| |||||||||||||||
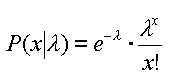 | |||||||||||||||
mit | |||||||||||||||
| |||||||||||||||
und | |||||||||||||||
x = Fehler pro Einheit (x = 0, 1, 2, ...) bestimmt. | |||||||||||||||
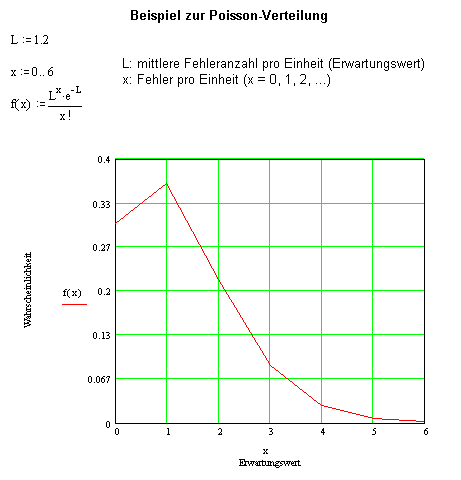
Die mittlere Fehlerzahl ist der arithmetische Mittelwert der Fehler einer großen Zahl “Einheiten”. Mit steigendem Erwartungswert nähert sich die Poisson-Verteilung einer Normalverteilung. 1. Beispiel: Der Fehlererwartungswert | |||||||||||||||
a) genau 0, b) genau 2 oder c) höchstens 2 | |||||||||||||||
Lackfehler pro Bauteil vorzufinden? Berechnung der Wahrscheinlichkeit P für a) genau 0 Fehler: | |||||||||||||||
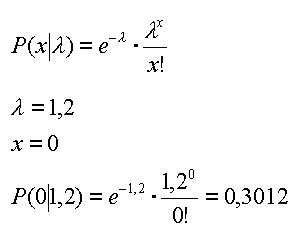 | |||||||||||||||
Die Wahrscheinlichkeit P(0|1,2) beträgt 0,3012 oder 30,1%. Berechnung der Wahrscheinlichkeit P für b) genau 2 Fehler: | |||||||||||||||
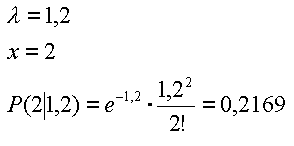 | |||||||||||||||
Die Wahrscheinlichkeit P(2|1,2) beträgt 0,2169 oder 21,7%. Zur Berechnung von c) höchstens 2 Fehler, wird noch die Wahrscheinlichkeit für genau 1 Fehler pro Einheit benötigt: | |||||||||||||||
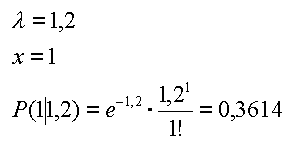 | |||||||||||||||
Höchstens 2 Fehler pro Bauteil ist die Summe der Wahrscheinlichkeiten PSum: | |||||||||||||||
PSum = P(0) + P(1) + P(2) PSum(2|1,2) = 0,3012 + 0,3614 + 0,2169 = 0,8795 = 87,95% | |||||||||||||||
Lösung über Mathcad: | |||||||||||||||
 | |||||||||||||||
Lösung über das Statistiklabor: (Beispiel als Zip-Datei laden....) | |||||||||||||||
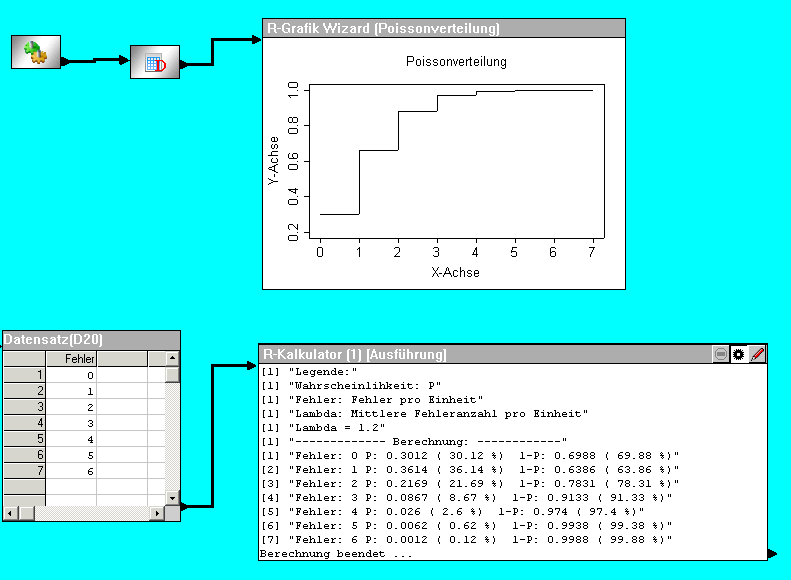 |
In obiger Grafik “Poisonverteilung”, sie wurde zufällig auf Basis von Lambda 1,2 erzeugt, wird der diskrete Charakter deutlich. Additionssatz der Poisson-Verteilung: Ist die Fehleranzahl |
ebenso poissonverteilt. 2 Beispiel: In diesem Beispiel werden 3 Einheiten des 1. Beispiels, mit dem Erwartungswert |
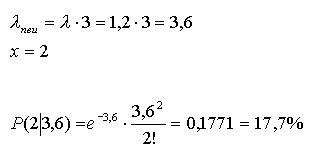 |
Die Differenz beträgt 4%. Hier muss also eine Entscheidung zwischen Stichproben- und Arbeitsumfang getroffen werden. |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |