 |
Kombinationen ohne Wiederholung, Binomialkoeffizient, k-Permutation |
Unter
Kombinationen ohne Wiederholungen wird die Auswahl von k Elemente aus einer Menge G von n Elementen in einer beliebigen Reihenfolge, aber ohne Wiederholung der Reihenfolge, verstanden. |
Wie oft können aus n = 7 Elemente auf verschiedne Weisen Gruppen von k = 3 Elemente, deren Reihenfolge belanglos ist (ungeordnet, ohne Wiederholung), gebildet werden? |
|
|
Die Elemente 1, 2, 3 besitzen die Anordnung 3! von den möglichen 7! Anordnungen (siehe Permutation). Obige Frage lässt sich mit |
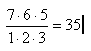 |
|
beantworten. Nun ist obiger Bruchstrich für die alltäglich Schreibweise zu umständlich und deswegen wird er als Binominalkoeffizient dargestellt: |
|
| ||||||||||||||||||||
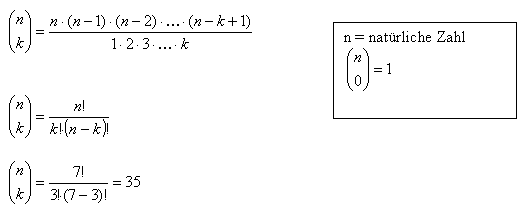 |
Aus 7 Elementen können 35 Gruppen bestehend aus 3 Elemente kombiniert werden. Häufig verwendete Schreibweisen sind auch |
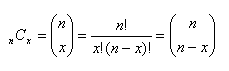 |
mit 0 <= x <= n und x, n sind ganzzahlig. |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |