
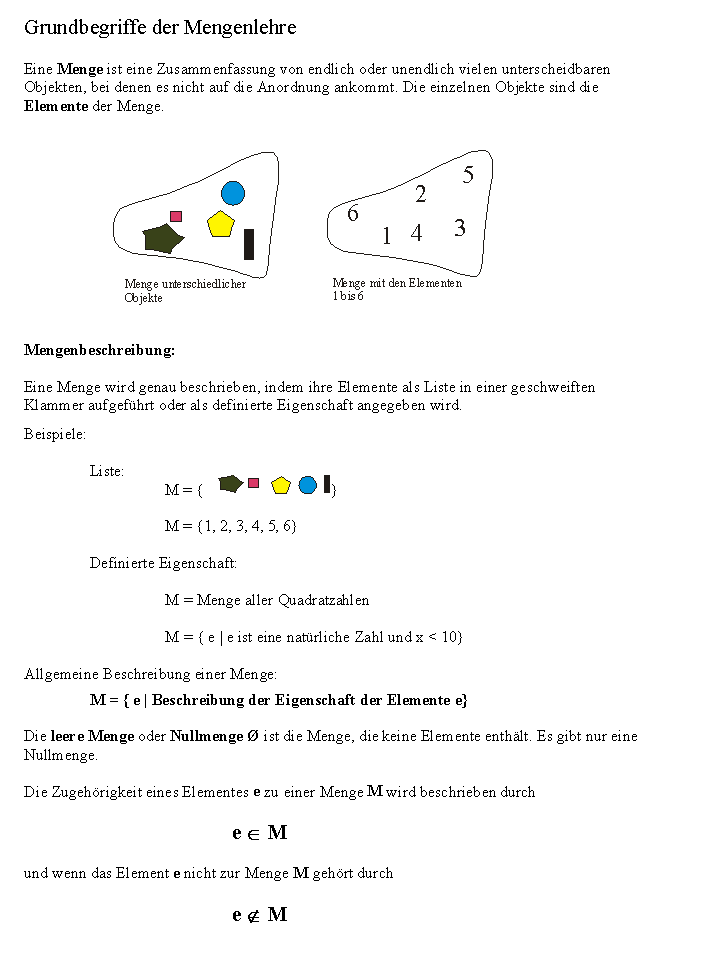
 | |||||
 |
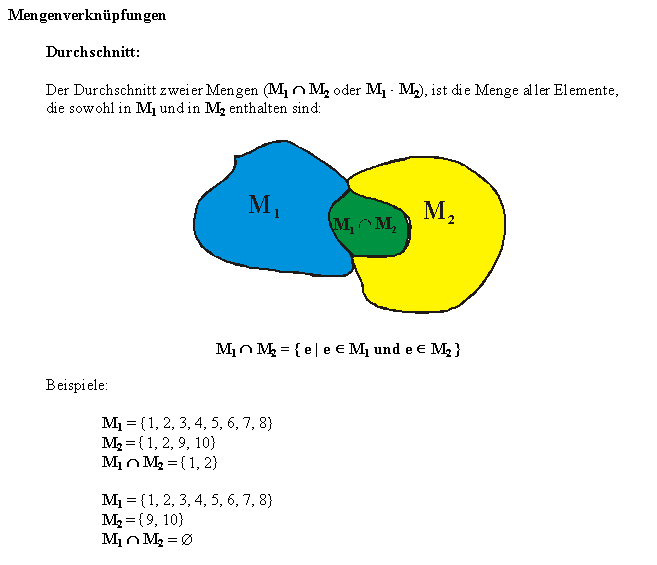
 | |||||||
 | |||||||
Für die letzte Menge der obigen Beispiele, für Mengen die keine gemeinsamen Elemente besitzen,
also für | |||||||
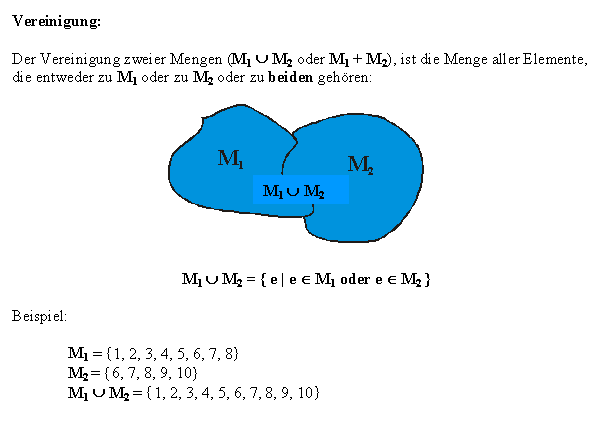 | |||||||
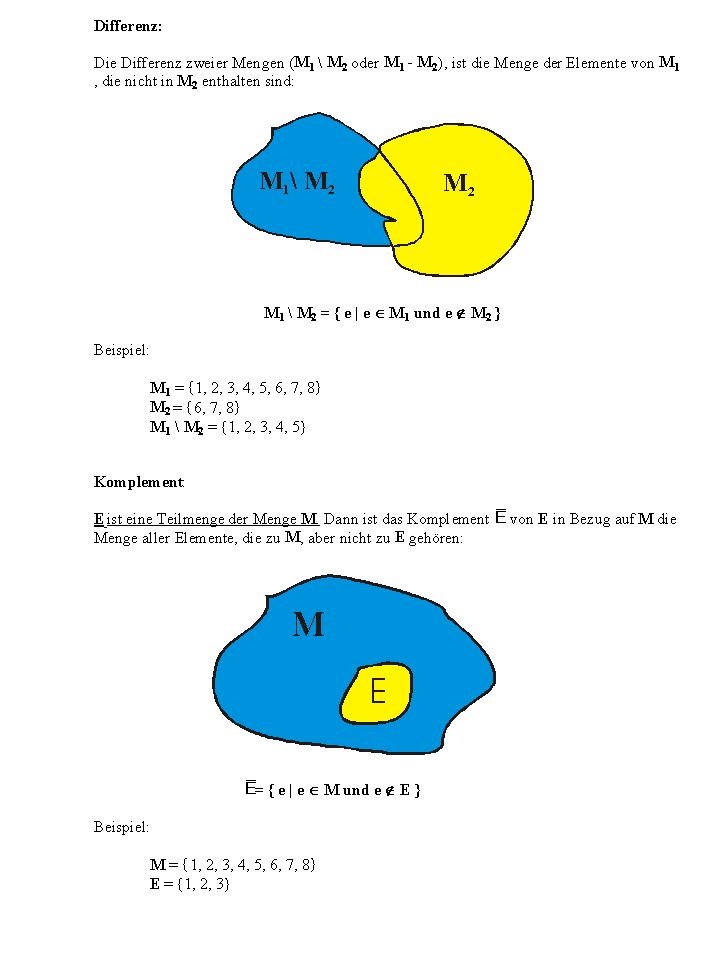 |
Mächtigkeit einer Menge: Die Anzahl der Elemente einer Menge M heißt Mächtigkeit von M und wird mit Potenzmenge: Bei den Potenzmengen geht es um die Menge aller Teilmengen. M ist ein nichtleere Menge. Die Menge aller
(verschiedenen) Teilmengen von M, inklusive der leeren Menge, heißen Potenzmenge von M wird mit Beispiel:
Die Potenzmenge |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |