 |
| ||||||||||||||||||
Matrix-Typen Eine Matrix M mit m Zeilen und n Spalten ist eine Matrix vom Typ M(m,n). Eine Matrix, in der die Anzahl der Zeilen gleich der Anzahl Spalten ist, ist eine quadratische Matrix: |
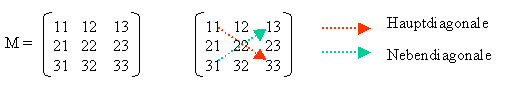 |
Eine Matrix vom Typ M(1,n) wird Zeilenvektor und eine Matrix vom Typ M(m,1) wird Spaltenvektor genannt: |
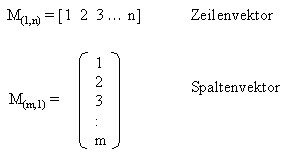 |
Transponierte Matrix (gestürzte Matrix) Werden in einer Matrix M(m,n) die Zeilen gegen die Spalten vertauscht (oder umgekehrt), erhält man die transponierte Matrix MT(n,m): |
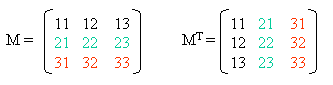 |
Die transponierte Form des Zeilenvektors ist der Spaltenvektor M(1,n) = MT(m,1) und die des Spaltenvektors der Zeilenvektor M(m,1) = MT(1,n) . Die transponierte Form einer transponierten Matrix ist die ursprüngliche Matrix: |
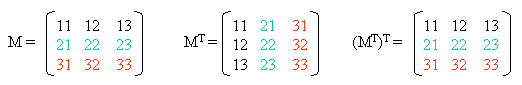 |
Bemerkungen zur quadratischen Matrix Symmetrische Matrix: |
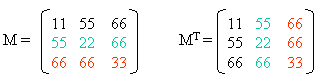 |
Antisymmetrische Matrix: |
|
|
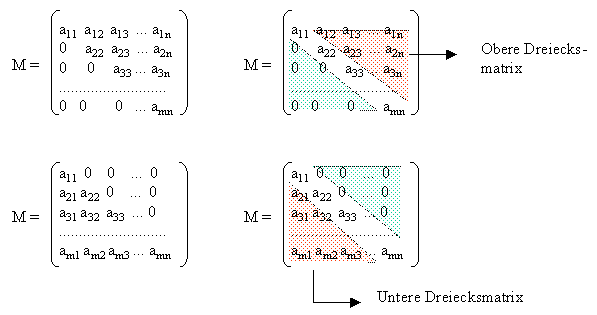
Dreiecksmatrix: |
 |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |