Potenzen und Co.

Einen Ausdruck der Form x^y wird als Potenz bezeichnet, wobei x die Basis und y der Exponent darstellt. Die Potenz x^y ist für alle positiven reellen Zahlen x und allen reellen Zahlen y definiert. Folgende Regeln gelten:

In Abbildung 1 wurde die Umkehrfunktion des Potenzierens, das Wurzelziehen eingeführt:

a ist der Radikand und n der Wurzelexponent . Für 7 in Abb.1 gilt, dass z eine positive ganze Zahl > 1 ist (siehe auch hier). Als Ergänzung zu 6 gilt

und zu 7

Der Compagnon der Potenz ist der Logarithmus. Um hier eine Beziehung herzustellen, müssen Sie sich nur in Erinnerung rufen, dass Logarithmus eine andere Bezeichnung für Exponent ist.

Nehmen wir zur Erklärung das Beispiel 5^x = 125. Der Logarithmus ist die Zahl x, mit der 5 potenziert werden muss um 125 zu erhalten: x = log₅ 125.

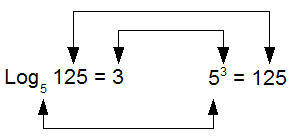Abb. 2

Oder wie in Abbildung 3 allgemein formuliert:

Ist a > 1 und b < 0, dann ist die Lösung der Gleichung a^x = b der Logarithmus x von b zur Basis a, x = log_ab.

Abbildung 4 zeigt die Nomenklatur zum Logarithmus:

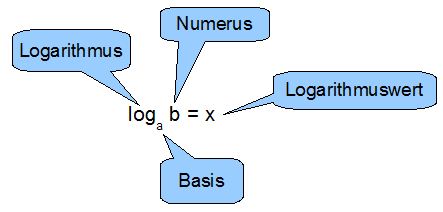Abb. 4

In der Praxis wird als Basis e = 2,71828... (natürlicher Logarithmus) oder der dekadische Logarithmus zur Basis 10 verwendet.

Wie mit Logarithmen gerechnet wird, zeigt folgendes Beispiel:

Mehr zum Thema Logarithmus siehe Regressionsanalyse!

Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?