 |
| ||||||||||||||
(t-Test für paarweise angeordnete Messwerte) |
Dieser Test beantwortet die Frage, ob 2 parallele unabhängige Datenreihen xi und xj als Merkmalsergebnisse von z. B. einem Material (chemische Substanz) auf Basis von unterschiedlichen Prüfmethoden ermittelt wurden, einer Grundgesamtheit entstammen. Oder anders formuliert: Sind beide Datenreihen xi und xj von einander abhängig oder unabhängig? Die Prüfung wird wie folgt durchgeführt: Die Prüfgröße PG wird berechnet aus dem Mittelwert |
 |
4. Die Nullhypothese ist H0: xi = xj und diese trifft zu, wenn PG <= t(P, f), was bedeutet, dass kein Unterschied zwischen den Datenreihen vorliegt. | ||||
Die Alternativhypothese ist H1: xi # xj und sie trifft dann zu, wenn PG > t(P, f). Dann liegt ein Unterschied zwischen den Datenreihen vor. Die Merkmalsergebnisse entstammen unterschiedlichen Grundgesamtheiten. | ||||
Beispiel: | ||||
Folgende Datenreihen xi und xj sollen darauf geprüft werden, ob sie der gleichen Grundgesamtheit entstammen: |
| |||||||||||||||||||||||||||||||||||||||||
Berechnung der Prüfgröße PG: | |||
Der Vergleichswert der t-Verteilung t(P=95%, f=6, zweiseitig) = 2,447 |
Da die Prüfgröße PG 7,94 größer ist als der Vergleichswert t, muss davon ausgegangen werden, dass die Datenreihen unterschiedlichen Grundgesamtheiten entstammen und die Alternativhypothese H1 zutrifft: | |||
PG (7,94) > t (2,447) | |||
Bemerkungen:
|
Mit dem Sollwert-t-Test, als Variante des Differenz-t-Tests, prüfen Sie, ob der beobachtete (gemessene) Mittelwert einer Datenreihe dem Sollwert entspricht oder sich signifikant unterscheidet. D. h., die Fragestellung lautet, wird der Sollwert für die aktuellen Beobachtungen eingehalten oder nicht? Die Prüfung wird wie folgt durchgeführt: Gegeben ist ein Sollwert von 95,0 %, den ein Produkt bezüglich seines Wirkstoffgehaltes erreichen soll. Von der aktuell produzierten Charge wird eine Stichprobe mit dem Stichprobenumfang 7 entnommen und auf den Wirkstoffgehalt hin analysiert: |
|
Es wird Normalverteilung angenommen. Es soll nun geprüft werden, ob der Sollwert 95,0 % eingehalten wird. Die Hypothese H0 lautet H0: also keine signifikante Abweichung vom Sollwert. In diesem Beispiel liegt eine Abweichung d von d = |
vor. Ist diese Abweichung d so klein, dass die Hypothese H0 aufrecht erhalten werden kann, oder ist sie so groß, dass H0 abgelehnt werden muss? Die Alternativhypothese H1 dazu lautet dann, dass der Mittelwert H1: In diesem Fall wird von einem Alternativtest gesprochen und in diesem Zusammenhang spielt der Fehler 1. Art bzw. Fehler 2. Art eine Rolle. Die Prüfgröße PG zur Hypothesenprüfung wird wie folgt berechnet (siehe auch 3. oben): |
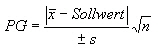 | |||
Die Prüfgröße PG wird mit dem t-Wert der t-Verteilung für die gewünschte statistische Sicherheit P und dem entsprechenden Freiheitsgrad f verglichen. In diesem Beispiel gehen wir von einer statistischen Sicherheit von P = 95 % (oder 0,95) und einem Freiheitsgrad f = 7 -1 = 6 aus. H0 trifft dann zu, wenn H0: PG <= t(P,f), H0: PG <= t(0.95, 6) ist. Der t(0.95, 6)-Wert (zweiseitig) beträgt 2,447 und wegen 0,441 < 2,447 trifft H0 zu, d. h., der aktuell vorliegende Mittelwert entspricht mit einer 95 %igen statistischen Wahrscheinlichkeit dem Sollwert von 95,0 %. Auch hier lässt sich das Statistikprogramm R als Hilfsmittel einsetzen. Auf der Konsole wird die Funktion t.test() wie folgt aufgerufen: > # x entspricht dem aktuellen datensatz Der durch R berechnete t-Wert -0.4201 unterscheidet sich durch den hier berechneten t-Wert 0,441 durch die Rundung der Abweichung d auf 0,03. Da der p-value = 0.689/2 > 0,025 (das zweiseitige Signifikanzniveau beträgt (1-0,95)/2) deutlich größer ist als das Signifikanzniveau (Irrtumswahrscheinlichkeit) muss davon ausgegangen werden, dass der aktuelle Mittelwert dem Sollwert entspricht. |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |