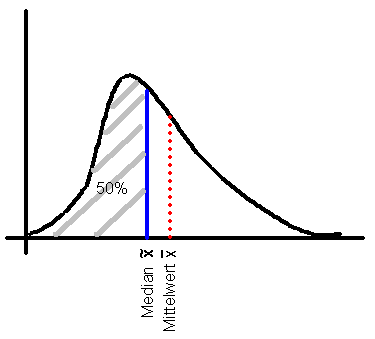
Median


	*Zurück...*


	Siehe auch *Mittelwert...*


	Median :


	Der Median stellt den Wert dar, der eine Verteilung in zwei gleich große Teile teilt. Der Median ist besonders interessant für schiefe Verteilungen, also solche, die von der Normalverteilung abweichen:


	Der Median eignet sich als Lokalisationsmaß für:


	mindestens ordinalskalierte Beobachtungen, nur wenige Messwerte, asymmetrische Verteilungen (siehe Grafik oben), für Verteilungen mit offenen Endklassen und bei Verdacht auf Ausreißer

Beispiele:

1. Beispiel, ordinalskalierte Beobachtung:

Eine der Größe nach geordnete Merkmalsreihe wird durch den Median , wenn die Anzahl der Merkmalswerte ungerade ist, in der Mitte geteilt:

Die Stelle des Medians wird für eine ungerade Anzahl wie folgt berechnet:

Stelle Median = (n+1)/2

Stelle Median = (7+1)/2

Stelle Median = 4


	Wenn die Anzahl der Merkmalsergebnisse *gerade* ist, wird der Median wie folgt berechnet:

Es wird der Mittelwert der Merkmalsergebnisse der Stellen (n/2) und (n/2+1) berechnet.

Anzahl n = 8

1. Stelle = (n/2) = 4
2- Stelle = (n/2+1) = 5

= (96,7+96,6)/2 = 96,65


	2. Beispiel, klassifizierte Merkmalsergebnisse:


	Der Median wird in der Klasse 96-98 erwartet. Die Häufigkeit h der Merkmalsergebnisse in dieser Klasse beträgt 18.


	Der Median wird klassierte Merkmalsergebnisse nach folgender Formel berechnet:


	KG_unten: Klassengrenze unten der Medianklasse b: Klassenbreite n: Anzahl der Werte : Summe der Häufigkeitswerte h aller Klassen unterhalb der Medianklasse h_Median: Anzahl der Werte in der Medianklasse


	Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?