 |
|
| ||||||||||||||||||||
In der Literatur wird dieses hier beschriebene Verfahren auch unter folgenden Begriffen beschrieben: Kleinste-Quadrate-Regression (OLS), K-Matrix, Classical Least Squares (CLS) |
Ausgehend vom Bouguer-Lambert-Beerschen-Gesetz verhalten sich die Extinktionswerte A der Einzelkomponenten additiv. Folglich lässt sich ein Spektrum, wie z. B. jenes aus der voran- gegangenen Seite, allgemein wie in folgender Gleichung darstellen: |
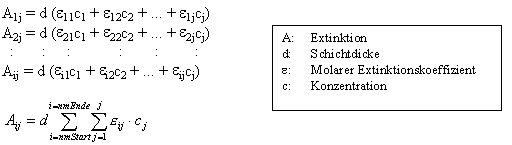 |
Die Schichtdicke d wird im Folgenden als Konstant mit 1(cm) angenommen. Auch wenn eine Küvette mit einer anderen Schichtdicke verwendet wird, spielt dies keine Rolle. Es muss nur beachtet werden, dass die Schichtdicke mit “einkalibriert” wird! Obige Gleichung wird übersichtlicher, wenn sie in der Matrixschreibweise dargestellt wird: |
|
|
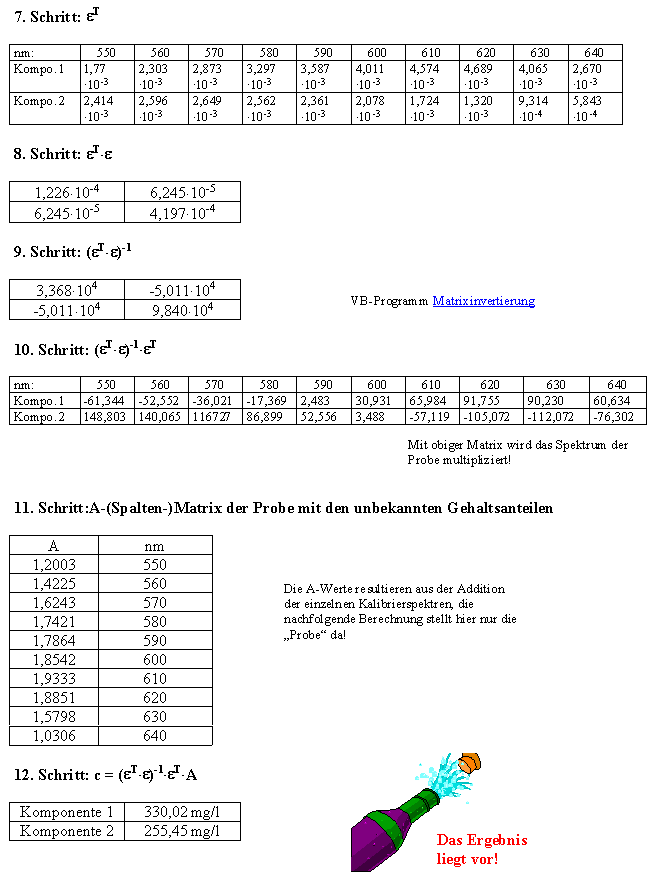
Mit Hilfe der Kalibriermessungen wird die Grundlage zur Bestimmung der e-Matrix, auf Basis der bekannten c-Matrix und der gemessenen A-Matrix, geschaffen: |
|
|
Nach dem die e-Matrix durch die Kalibrierung bestimmt wurde, sind wir nun in der Lage, von Mehrkomponenten-Spektren den Gehaltsanteil der Komponenten zu berechnen: |
 | |||||
 | |||||
 |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |