Zurück...

Allgemeines zur Algebra

Die Algebra beschäftigt sich mit dem Teilgebiet Gleichungen der Arithmetik. Unter einer Gleichung wird die Aussage verstanden, dass zwei arithmetische Ausdrücke (Terme) gleich sind, bzw. gefordert wird, dass die Ausdrücke gleich sein sollen. Das Kennzeichen einer Gleichung ist das =-Zeichen. Eine Gleichung wird also wie folgt geschrieben:

Ausdruck₁ = Ausdruck₂
oder
1 + 2 = 3

 Gleichungen werden unterschieden in

• Identische Gleichungen
  Eine identische Gleichung oder Identität ist eine Gleichung zwischen zwei Ausdrücken, die bei Einsetzen beliebiger Zahlenwerte anstelle der darin aufgeführten Symbole erhalten bleibt.
  Beispiele:
  a(b + c) = ab + ac
  a^m * aⁿ = a^m+n
  (a + b)² = a² + 2ab + b²
   
• Bestimmungsgleichungen
  In Bestimmungsgleichungen treten Variable (Unbekannte) auf, die durch Berechnungen bestimmt werden sollen. Die Lösung einer Bestimmungsgleichung ist ein bestimmter Wert (Zahl) oder ein bestimmter Zahlenbereich für den die Gleichung erfüllt ist. Diese Zahl oder Zahlenbereich wird Lösungsmenge L der Bestimmungsgleichung genannt.
  Beispiel:
  x + 5 = 8  Lösung: x = 3, Lösungsmenge: L = {3}
   
• Funktionsgleichungen
  In Funktionsgleichungen wird ein Zusammenhang zwischen veränderlichen Größen beschrieben.
  Beispiel:
  Umfang U = Pi * d   (d: Durchmesser der beliebige positive Werte annehmen kann)
   
• Ungleichungen
  In einer Ungleichung steht statt des Gleichheitszeichen “=” einer Gleichung, eines der Symbole

In einer Äquivalenzumformung können Ungleichungen genauso behandelt werden, wie Gleichungen. Allerdings mit einer wichtigen Ausnahme:
Bei einer Multiplikation mit einem negativen Ausdruck ändert sich die Richtung der Ungleichung:

Für Summen oder Differenzen gilt die Dreiecksgleichung:

Unterteilt werden Bestimmungsgleichungen in algebraische und transzendente Gleichungen. In algebraischen Gleichungen werden mit den Variablen nur algebraische Rechenoperationen, wie Addieren, Subtrahieren, Multiplizieren, Dividieren, Potenzieren und Radizieren durchgeführt. Die Koeffizienten und die Lösungen können transzendente Zahlen sein.
Transzendente Gleichungen sind Exponentionalgleichungen, logarithmische und trigonometrische Gleichungen.
Algebraische Gleichungen mit einer Variablen x lassen sich in der allgemeinen Form

a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ... + a₁x + a₀ = 0

darstellen. In obiger allgemeinen Form sind a_n, ..., a₀ Koeffizienten, die beliebige reelle oder komplexe Zahlen sein können.
Die Variable xⁿ ist die höchste auftretende Potenz der Variable x und die Gleichung heißt dann Gleichung vom Grad n:

• a₁x + a₀ = Gleichung vom Grad 1 = lineare Gleichung
• a₂x² + a₁x + a₀ = Gleichung vom Grad 2 = quadratische Gleichung
• a₃x³ + a₂x² + a₁x + a₀ = Gleichung vom Grad 3 = kubische Gleichung

Jede algebraische Gleichung n-ten Grades hat genau n Lösungen.

Äquivalente Umformungen

Durch Umformen einer komplizierten Form einer Gleichung mit zulässigen Rechenoperationen kann sie in eine Form überführt werden, die leichter zu lösen ist. Selbstverständlich muss die umgeformte Gleichung die gleiche Lösungsmenge wie die Ausgangsgleichung besitzen. Trifft dies zu, ist die Umformung äquivalent und die beiden Gleichungen sind dann äquivalent (gleichwertig).

Die Rechenoperationen werden gleichzeitig auf beiden Seiten der Gleichung durchgeführt:

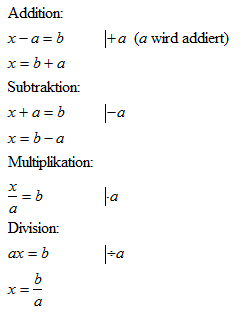Ein Beispiel für ein Nicht-Äquivalenzumformung ist das Quadrieren, da die Quadratwurzel doppeldeutig ist:

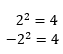Es sollte immer geprüft werden, ob die durchgeführte Umformung auch immer in die umgekehrte Richtung durchgeführt werden kann!

Lineare Gleichungen

Eine lineare Gleichung ist eine algebraische Gleichung, in der die Variable x in keiner höheren Potenz als der ersten Potenz (= Gleichung 1. Grades) vorkommt:

Obige lineare Gleichung ist die allgemeine Form der linearen Gleichung. Die Normalform der linearen Gleichung wird erhalten, indem sie durch a (a # 0) dividiert wird:

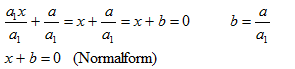Die Lösung ist dann

und die Lösungsmenge somit

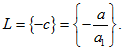Beispiel:

Proportionen

Eine Proportion ist eine Verhältnisgleichung und besetzt aufgrund ihrer Vielseitigkeit eine besondere Position unter den linearen Gleichungen. Das Verhältnis 3/6 hat den gleichen Wert, wie 6/12 und deswegen können beide Verhältnisse als Gleichung geschrieben werden:

Obige Gleichung wird deswegen Verhältnisgleichung oder Proportion genannt.

Allgemein wird die Proportion wie folgt dargestellt:

Ausgehend von der Form a : b = c : d heißen

a und d Außenglieder,
b und c Innenglieder,
a und c Vorderglieder und
b und d Hinterglieder.

Eine Proportion kann eine identische Gleichung, eine Bestimmungsgleichung oder eine Funktionsgleichung sein. Für Proportionen gelten die allgemeinen Gesetze für das Rechnen mit Gleichungen.

Sind von den Gliedern einer Proportion drei bekannt, lässt sich die Proportionale (das vierte Glied) berechnen:

Proportionen lassen sich umformen und folgende Beispiele sind äquivalente Formen von  a : b = c : d :

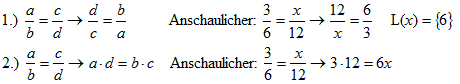Die Umformungsbeispiele sind nicht komplett dargestellt. Erwähnenswert sind noch die korrespondierenden Umformungen (ebenfalls nicht vollständig):

Quadratische Gleichungen

Eine quadratische Gleichung oder Gleichung zweiten Grades ist eine algebraische Gleichung, in der die Unbekannte x in keiner höheren als der 2. Potenz vorkommt. Über geeignete Rechenoperationen lässt sich jede quadratische Gleichung mit einer Unbekannten in die allgemeine Form

bringen. Die drei Glieder der allgemeinen Form heißen

ax² das quadratische Glied,
bx das lineare Glied und
c das absolute Glied.

Durch Division der allgemeinen Form mit a (a # 0) erhält man die Normalform der quadratischen Gleichung, die i. d. R. wie folgt geschrieben wird:

• Reinquadratische Gleichung

Eine quadratische Gleichung, in der das lineare Glied fehlt, wird reinquadratisch genannt:

Beispiel und Lösung einer reinquadratischen Gleichung:

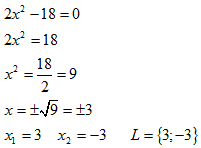Die Quadratwurzel ist in Bezug auf das Vorzeichen doppeldeutig (siehe auch komplexe Zahlen) und deswegen muss beim Radizieren das doppelte Vorzeichen berücksichtigt werden. Daher besteht die Lösungsmenge L aus zwei Lösungen L{x₁; x₂}. Im obigen Fall erfüllt x₁ und x₂ die Ausgangsgleichung.

Im folgenden Beispiel sieht es anders aus:

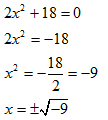In diesem Falle gibt es keine reelle Lösung, sondern eine komplexe Lösung (siehe komplexe Zahlen):

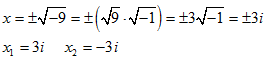Daraus folgt, dass eine reinquadratische Gleichung entweder zwei reelle oder zwei komplexe Lösungen hat.

• Gemischtquadratische Gleichung ohne absolutes Glied

Eine quadratische Gleichung mit einem linearen Glied, wird gemischtquadratisch genannt. Auch wenn, wie im folgenden Beispiel, das Absolutglied fehlt:

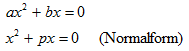Über Ausklammern

wird erkannt, dass das Produkt x(x + p) genau dann gleich 0 ist, wenn einer der beiden Faktoren gleich 0 ist. Ist x = 0, dann ist die Lösung x₁ = 0 und x₂ = -p.
Um eine Lösung zu erhalten, darf nicht durch x dividiert werden. Sonst geht dabei die Lösung x = 0 verloren!

Daraus folgt, dass eine gemischtquadratische Gleichung ohne Absolutglied immer zwei reelle Lösungen hat, von denen eine 0 ist.

• Gemischtquadratische Gleichung

Unter einer gemischtquadratischen Gleichung wird

oder die Normalform

verstanden.

Beispiel:

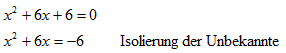Die beiden links stehenden Glieder der obigen Gleichung werden durch Addition einer geeigneten Zahl zu einem vollständigen Quadrat wie a² + 2ab + b² ergänzt:

Die quadratische Ergänzung, die zum Erreichen eines vollständigen Quadrates noch fehlt, entspricht b². Für dieses Beispiel also b² = 3² = 9. Die quadratische Ergänzung ist hier die Zahl 9:

• Formellösung einer gemischtquadratischen Gleichung

Über die Normalform der gemischtquadratischen Gleichung lässt sich die formelmäßige Lösung ableiten:

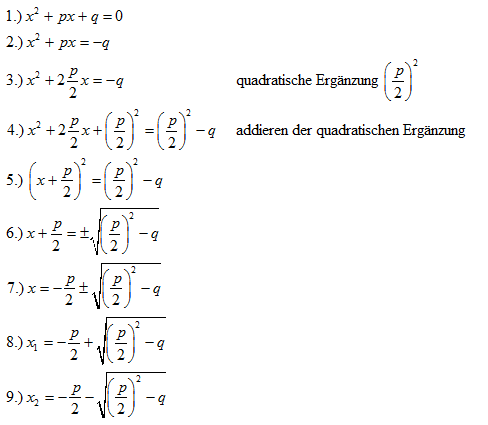Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?