|
| |
 |
| | | |
| |||
Die χ2-Verteilung lässt sich als Verteilung der Summe von unabhängigen quadrierten standardnormalverteilten Zufallsvariablen herleiten und ist nur abhängig vom Parameter df, dem Freiheitsgrad (df = n – 1):
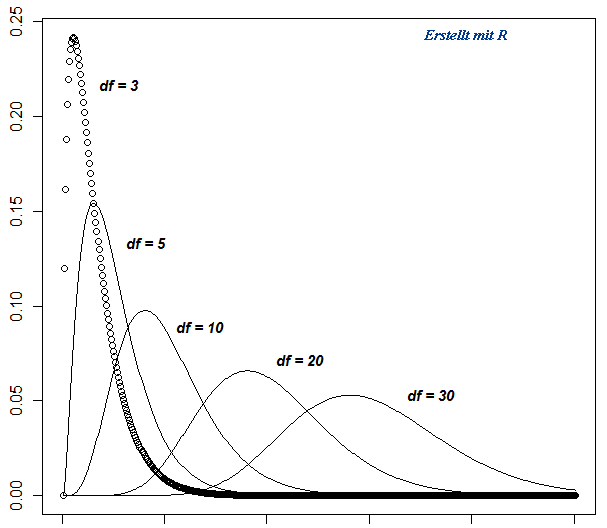
Sie ist eine stetige unsymmetrische Verteilung und erstreckt sich von 0 bis Unendlich und näher sich mit wachsendem Freiheitsgrad einer Normalverteilung an. Das heißt, mit größer werdenden Freiheitsgrad df wird die Kurve flacher und symmetrischer: | |||
| |
 |
| |
Die χ2-Verteilung dient zur Prüfung der Übereinstimmung z. B. zwischen beobachteter und theoretischer Verteilung, siehe χ2-Test. |
| |
 |
| |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |
|
|
-Verteilung (Chi2-Verteilung)