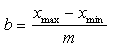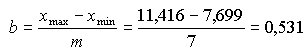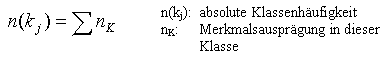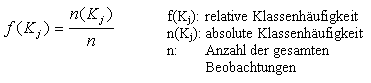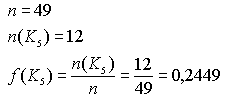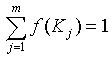Klassenbildung Die Klassenbildung (Klassierung, Kategorisierung) von stetigen Daten (Merkmalsausprägungen) in Klassen (K1, ... Km) ist eine
Datenzusammenfassung (Komprimierung), um durch dann die erhaltene Strukturierung eine Aussage über deren Häufigkeitsverteilung machen zu können. Die Komprimierung ist von der Anzahl der Klassen abhängig, d. h., ist die Anzahl zu klein, also wenige Klassen, gehen vielleicht zu viele Informationen verloren und ist sie zu groß, also zu viele Klassen, könnte die Struktur verloren gehen.
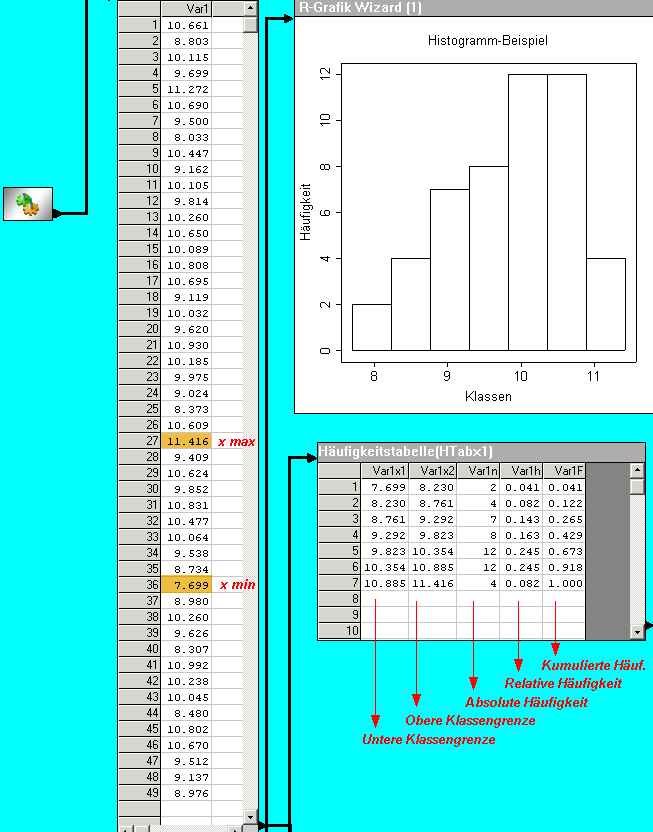
Diese Klassierung kann dann natürlich auch als Histogramm grafisch dargestellt werden und ist dadurch wesentlich anschaulicher. Um die Daten klassieren zu können, muss der Datenbereich (Ergebnisraum), xmin bis xmax in eine vorgegebene Klassenanzahl m
(Intervalle) eingeteilt werden. Die Länge dieser Intervalle wird als Klassenbreite b bezeichnet und sie sollte für jedes Intervall gleich groß, äquidistant, sein. Die äquidistante Klassenbreite b ist von der Klassenanzahl m abhängig und neben der subjektiven Schätzung von m sollte folgende Faustregel angewendet werden: |