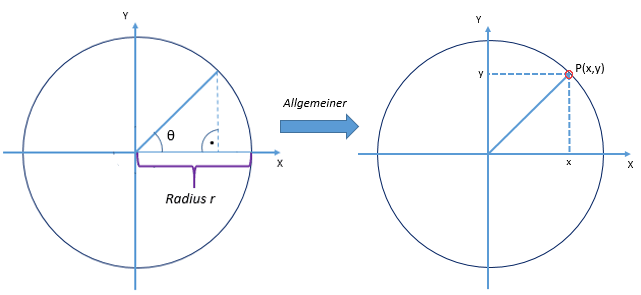
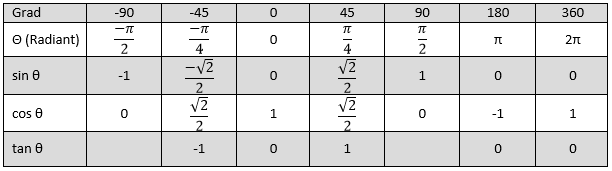
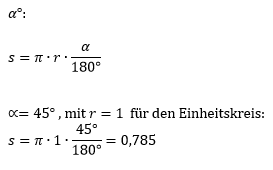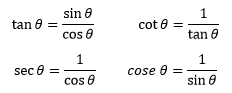Eine Funktion f(x) ist periodisch, wenn
mit p als positive Zahl. Der kleinste Wert von p ist die Periode von f. Die folgende Abbildung zeigt ein Periodizitätsbeispiel für die Funktionen y = sin(x) und y = cos(x): Die Graphen der Funktionen y = sin(x) und y = cos(x) haben die gleiche Form, sind lediglich um den 1/2 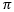 gegeneinander verschoben. Der Funktionsverlauf wiederholt sich nach einem Intervall von 2
gegeneinander verschoben. Der Funktionsverlauf wiederholt sich nach einem Intervall von 2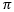 , das heißt, die Periode ist 2 , das heißt, die Periode ist 2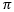 (Wellenlänge oder Schwingungsdauer). (Wellenlänge oder Schwingungsdauer). Trigonometrische Identitäten Im Falle das r = 1 (Einheitskreis) ist, gilt dann für das (Referenz-)Dreieck im Einheitskreis bei Anwendung des Satzes des Pythagoras die Gleichung
Daraus abgeleitet durch Division mit 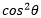 bzw. bzw. 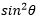 erhält man erhält man
Die folgenden Gleichungen gelten für alle Winkel 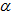 und und 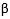 : : Die obigen Funktionsgrafiken wurden teilweise erstellt mit dem
Ti-Nspire Cx Casii-T
|