 |
Korrelations- und Regressionsanalyse Einleitung Die
Abhängigkeit zwischen zwei Merkmalen eines Objektes (Material, Prozess, ...) werden mit der Korrelations- und Regressionsanalyse untersucht (multivariate Analysenmethode). |
 |
Korrelationsanalyse Die Korrelationsanalyse untersucht Zusammenhänge zwischen Zufallsvariablen anhand einer Stichprobe. Eine Maßzahl für die Stärke und Richtung eines linearen Zusammenhanges ist der
Korrelationskoeffizient r. |
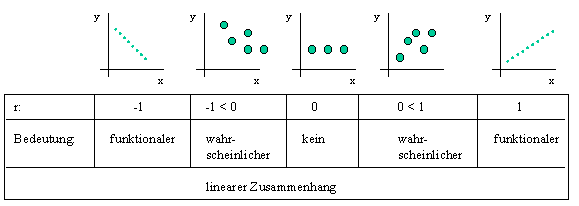 | |||
r = 0 bedeutet, dass kein Zusammenhang besteht. x und y sind voneinander unabhängig. Nähert sich r -1 oder 1 an, wird die lineare Abhängigkeit immer wahrscheinlicher. Ist r = -1 oder 1 liegt ein funktionaler linearer Zusammenhang vor (siehe auch Allgemeines zu Funktionen). Oft wird anstelle des Korrelationskoeffizienten r das Bestimmtheitsmaß r2 angegeben. Hier gilt, je näher das Bestimmtheitsmaß r2 an 1 liegt, desto höher ist die Wahrscheinlichkeit des linearen Zusammenhangs. Ist r2 = 0 liegt kein Zusammenhang vor. Das Bestimmtheitsmaß stellt also eine Maßzahl für die Güte der Anpassung dar und liegt im Bereich 0 =< r2 <= 1. Neben der Beurteilung des Bestimmtheitsmaßes über die Annäherung an 1, bietet sich der t-Test zur Prüfung der statistischen Signifikanz des vermuteten Zusammenhanges zwischen den Merkmalen x und y an. Nähres dazu finden Sie unter Test des Korrelationskoeffizienten. Durch die Regressionsanalyse wird die Abhängigkeit zwischen zwei Merkmalen (siehe auch multiple lineare Regression) eines Objektes einer Regressionsgleichung angepaßt: |
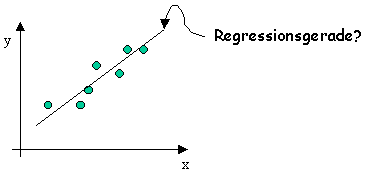 |
Besteht ein linearer Zusammenhang zwischen y und x - y ist das abhängige (Zufalls-) Merkmal und wird als Zielgröße bezeichnet, das Merkmal x ist die unabhängige Variable (Einflussgröße) - wird von linearer Regression gesprochen: y = a + bx Die Parameter a und b werden aus den Merkmalsdaten x und y nach der Methode der kleinsten Quadrate (auch Kleinst-Quadrate-Schätzung oder kurz KQ-Schätzung genannt) berechnet (geschätzt). Die Merkmalsausprägungen (die Daten) zur Einflussgröße x sind i. d. R. Zufallsgrößen und unterliegen demnach auch bestimmten Schwankungen e. Die obige lineare Funktion y = a + bx muss genau genommen um diese Abweichung (Zufallskomponente) e ergänzt werden (siehe auch Residuen): y° = a + bx + e
Näheres zu diesem Thema: Kovarianz und Standardabweichungen für a, b und r und siehe auch die Hinweise zu BLUE! |
Berechnung des Korrelationskoeffizienten r Wie in der Einleitung schon erwähnt, ist die im Folgenden aufgeführte Berechnung eine Schätzung des “wahren” Korrelationskoeffizienten r. Je größer der Stichproben- (Merkmals-) Umfang n ist, desto besser ist möglicherweise die Schätzung von r (wie oben schon angedeutet, siehe BLUE). Sind die Beobachtungen, die Merkmale, vom metrischen Skalenniveau, wird Korrelationskoeffizient nach Pearson geschätzt: |
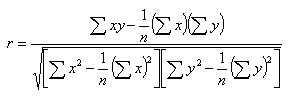 |
|
|
|
|
Das lineare Bestimmtheitsmaß r2 für dieses Beispiel beträgt 0,993272 = 0,9866. Wie weiter oben erwähnt, ist das Bestimmtheitsmaß r2 ein Gütemerkmal für die Anpassung. Es beinhaltet eine Varianzinformation, nämlich das Verhältnis zwischen unerklärter Varianz und Gesamtvarianz:
In diesem Beispiel mit r2 = 0,9866 kann 98,66 % der Varianz durch die Anpassung der Y-Werte an die Regressionsgerade erklärt werden und 1,34 % nicht. 1,34 % repräsentiert also die unerklärte Varianz.. |
Berechnung der Parameter a und b Die Parameter a und b sind Ihnen sicher geläufig unter den Begriffen für a gleich Schnittpunkt mit der y-Achse und b gleich der Steigung der Geraden |
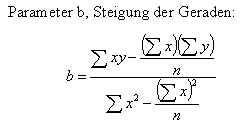 | 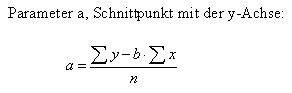 | ||||
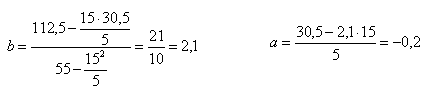 | |||||
Ergebnis der Korrelations- und Regressionsanlayse y = a + bx y = -0,2 + 2,1x mit r = 0,99327 oder r2 = 0,9866 Mit obiger linearer Funktion können nun bei gegebenem x-Wert (Merkmalswert) Voraussagen über y gemacht werden. Oder einfach ausgedrückt: y kann berechnet werden! Ist das Skalenniveau der Variablen binär oder auch mehrkategorial, dann siehe auch hier! Das Thema Modellanpassungen über Splines (flexible Modellierung) wird hier behandelt und die Modellsuche über Regressions- und Klassifizierungsbäume (Entscheidungsbaum) hier! |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |