t-Test zur Prüfung des Korrelationskoeffizienten r

Über den t-Test zur Prüfung der Korrelationskoeffizienten kann geprüft werden, ob ein statistisch signifikanter Zusammenhang zwischen den Ausprägungen (Realisierungen) x_i und y_i der Merkmale X und Y besteht.
Mit diesem Test können Sie nun neben Ihrer Einschätzung z. B. des Bestimmtheitsmaßes, eine statistisch gesicherte Aussage über die Güte des Zusammenhangs machen.

Sind die Merkmale normalverteilt, folgt die zu berechnende Prüfgröße PG einer t-Verteilung mit einem Freiheitsgrad f von f = n - 2 (n: Anzahl der Ausprägungspaare).
Ist der Absolutwert der berechneten Prüfgröße größer als der Tabellenwert t der t-Verteilung zweiseitiger Test), dann wird von einem statistisch gesicherten Zusammenhang, mit einer bestimmten Wahrscheinlichkeit P, ausgegangen.

Berechnung der Prüfgröße PG:

Wenn PG > t_{(f, P)} dann besteht ein Zusammenhang zwischen den Merkmalen X und Y.

Beispiel:

Ausgehend von dem Beispiel der Seite Korrelations- und Regressionsanalyse liegt uns folgender Korrelationskoeffizient r und folgendes Bestimmtheitsmaß r² vor:

r = 0,99327

r² = 0,9866

n = 5 (Anzahl Datenpaare)

In obige Formel eingetragen...

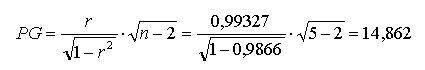... wird eine Prüfgröße von PG = 14,862 berechnet. Der Vergleichswert beträgt t_(f=3,P=98%) = 4,541 und somit liegt ein statistisch gesicherter Zusammenhang zwischen den Merkmale X und Y vor:

Zwischen X und Y besteht ein Zusammenhang, weil PG 14,862 > 4,541 t_(f=3,P=98%).

Unsere Erwartung aufgrund des Bestimmtheitsmaßes wird durch diesen Test bestätigt.

Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?