 |
Kreuz- oder Kontingenztabelle: Eine methodische Einführung in eine 2x2-Kontingenztabelle zeigt auch das YouTube-Video “Vierfeldertafel und R”. Über Kontingenztabellen können zwei Merkmale X und Y, z. B. ein ordinal- mit einem nominalskalierten (siehe Skalen), in Beziehung gebracht werden, um die Zusammenhänge der
Merkmalsausprägungen strukturiert als Häufigkeiten h (siehe Klassenbildung) darstellen zu können (multivariate Analysenmethode). |
|
| ||||||||||||||||||||
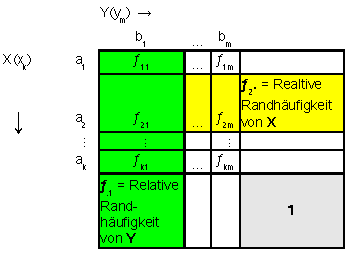
Werden Kontingenztabellen durch Spalten- und Zeilensummen, den sog, Randhäufigkeiten der Merkmale X und Y, ergänzt, können weitere Zusammenhänge sichtbar gemacht werden: |
 | ||
Abb. 3 | ||
Die Berechnung der oben berechneten absoluten Randhäufigkeiten h(X,Y) erfolgt nach folgendem Schema und Formel: |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
Die relative Darstellung der Häufigkeiten der Merkmalsausprägungen in Kontingenztabellen sind oft anschaulicher: |
 | |||||||||
Abb. 5 | |||||||||
Brechnung der realtiven Häufigkeiten: | |||||||||
 | |||||||||
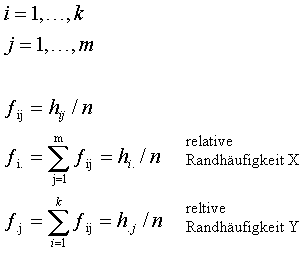 | |||||||||
Abb. 6 | |||||||||
Mit den bisher gezeigten Kontingenztabellen konnte die Auswirkung des Ausbildungsniveau auf die Arbeitslosendauer befriedigend dargestellt werden. Um aber einzelnen Ausbildungsniveaus bezüglich der Dauer der Arbeitslosigkeit besser betrachten zu können, bietet sich die Darstellung der bedingte relative Häufigkeitverteilung über die Kontingenztabelle an: |
 |
Abb. 7 |
Im obigen Beispiel wurde jedes Zeilenelement, z. B. die Häufigkeit Kurz 52, durch die Zeilensumme (Randhäufigkeit X), 264 dividiert. So ist deutlich zu erkennen, dass unter den Arbeitslosen mit Hochschulabschluss der Anteil der Langzeitarbeitslosen sehr gering ist. | |||||||||
 | |||||||||
Abb. 8 | |||||||||
In den obigen Tabellen wurden bisher die Ausprägungen der Merkmale X und Y in einer geeigneten Weise dargestellt, um einen möglichen Zusammenhang über die Häufigkeitsverteilung zwischen ihnen zu erkennen. Als erster Schritt zur Prüfung wird nachfolgend der Chiquadrat-Test ( Auf Basis des obigen Beispiels, kann die Hypothese | |||||||||
H0 : Ausbildung und Dauer der Arbeitslosigkeit sind voneinander unabhängig | |||||||||
aufgestellt werden. Die Berechnung der |
|
|
Die erwartete Häufigkeit hEij wird über das Postulat der empirischen Unabhängigkeit berechnet: |
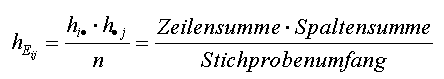 | ||
Erwartete Zellenhäufigkeit hEij | ||
Die Berechnung der erwarteten Häufigkeit hEij auf obige Ausgangsdaten in Abb.3 zeigt folgende Tabelle (Abb. 9): |
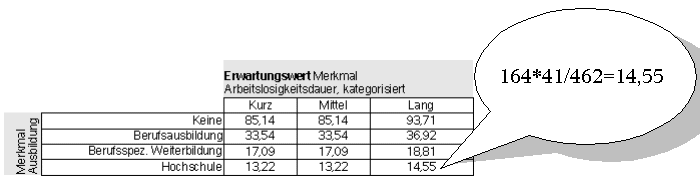 |
Abb. 9 |
Mit dem Vorliegen der erwarteten Häufigkeit hEij kann nun die |
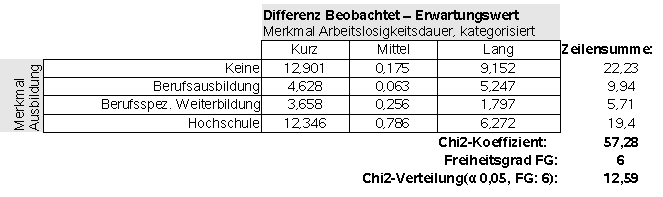 |
Abb. 10 |
In der Abb. 10 erkennen Sie neben der Von einem Vergleich der |
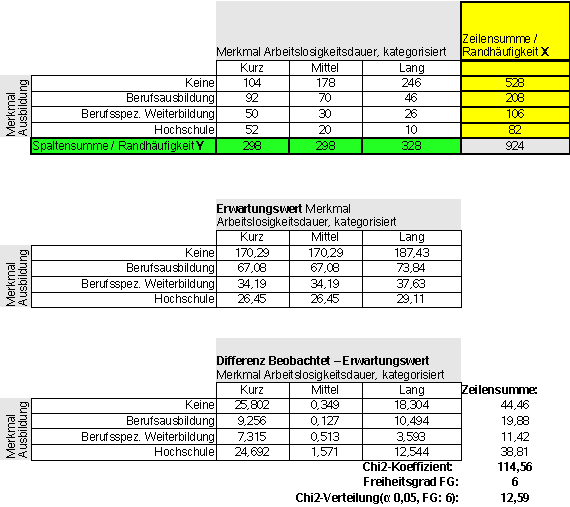 | |||
Abb. 11 | |||
|
|
Der Kontingenzkoeffizient K liegt im Wertebereich zwischen 0 und Kmax. Kmax als obere Grenze ist eine Funktion aus der Dimension der Tabelle, also abhängig von der Anzahl Spalten und Zeilen: |
|
|
Da K noch von der Dimension der Tabelle abhängt, ist ein weiterer Normierungsschritt hin zum korrigierten Kontingenzkoeffizienten K* nötig: |
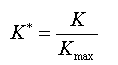 | |||
Der korrigierte Kontingenzkoeffizient K* liegt im Wertebereich zwischen 0 und 1 und ist nicht mehr von der Dimension der Kontingenztabelle abhängig. Auf obiges Beispiel bezogen, zeigt der korrigierte Kontingenzkoeffizienten K* eine Ausprägung von 0,407 (Abb. 12): |
 |
Abb. 12, korrigierter kontingenzkoeffizient K* |
| |||||||||||||||||
Der obige Beispieldatensatz wurde im R-Objekt Daten gespeichert (Abb. 13) ... |
 |
... und über die Funktion kontingenz die Schätzung des Korrigierten Kontingenzkoeffizienten durchgeführt: >
kontingenz(Daten) |
Sollte R Ihnen noch unbekannt sein, finden Sie einen Einstieg über das Buch Einführung in R. |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |