 |
| |||||||||||||||||||
Varianzanalyse | |||||||||||||||||||
Über die Varianzanalyse (ANOVA, Analysis of Variance)
wird der Einfluss eines oder mehrerer unabhängiger Merkmale (deren Ausprägung) auf ein bzw. mehrere abhängiger Merkmale geprüft. Es wird von einem Zusammenhang zwischen den Merkmalen ausgegangen. Also zählt diese Analysemethode zu den strukturprüfenden Verfahren. Z. B kann über die Varianzanalyse der Einfluss
verschiedener Einsatzstoffe auf die Ausbeute eines zu produzierenden Stoffes in der chemischen Industrie geprüft werden. Oder der Einfluss verschiedener Marketingstrategien auf den Absatz eines bestimmten Produktes. Hinweis: Die methodische Einführung in die Varianzanalyse zeigt auch das YouTube-Video “Varianzanalyse mit R”. Der Typ der Varianzanalyse unterscheidet sich durch die Zahl der Faktoren. Wird die Wirkung eines unabhängigen Merkmals auf ein abhängiges Merkmal geprüft, wird von einer einfaktoriellen Varianzanalyse gesprochen. Dabei wird für das unabhängige Merkmal von einem Faktor und für die Merkmalausprägung von einer Faktorenstufe gesprochen. Die folgenden Abbildungen zeigen beispielhaft unterschiedliche Typen der Varianzanalyse mit Wirkung auf ein abhängiges Merkmal: | |||||||||||||||||||
 | |||||||||||||||||||
 | |||||||||||||||||||
Abb. 2: Zweifaktorielle Varianzanalyse | |||||||||||||||||||
 | |||||||||||||||||||
Abb. 3: Dreifaktorielle Varianzanalyse | |||||||||||||||||||
Liegt mehr als eine unabhängige Variable vor, wird von einer mehrdimensionalen Varianzanalyse gesprochen: | |||||||||||||||||||
 | |||||||||||||||||||
Abb. 4: Mehrdimensionale Varianzanalyse | |||||||||||||||||||
Zunächst wird die Varianzanalyse über die einfaktorielle Varianzanalyse an folgenden einfachem Beispiel dargelegt. Später folgt dann als Beispiel die zweifaktorielle Varianzanalyse. Beispiel einfaktorielle Varianzanalyse In diesem Beispiel gehen wir von einer chemischen
Wirkstoffproduktion aus. Der Wirkstoff stellt ein Isomerengemisch aus 2. Isomere dar (Isomere: Chemische Verbindungen, die bei gleicher Summenformel verschiedene Strukturen und somit verschiedene chemische und physikalische Eigenschaften aufweisen.). Das Isomer I soll die aktive Komponente sein, d. h., auf dessen Gehalt (Merkmal) kommt es unserem “Kunden” an. | |||||||||||||||||||
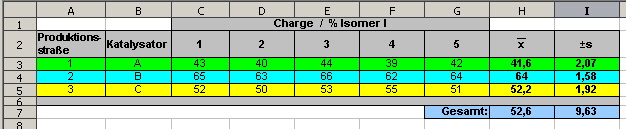 | |||||||||||||||||||
Abb. 5: Beispieldatensatz einfaktorielle Varianzanalyse |
Im obigen Beispiel ist der Katalysator das unabhängige Merkmal mit den Katalysatoren A bis C als Merkmalausprägung und das Isomer I ist das abhängige Merkmal mit der Merkmalsausprägung %-Gehalt. Bevor mit dem Text fortgefahren werden kann, muss zum Verständnis der folgenden Berechnungen etwas zur Notation der Daten in obiger Tabelle (Abb. 5) gesagt werden: |
|
Es sei noch einmal erwähnt, dass im Folgenden angenommen wird, dass keine äußeren Einflüsse für die Isomerenverteilung der Produktionsstraßen (Katalysatoren) verantwortlich sind, d. h., die Produktionsstrassen werden als gleich angesehen. |
Gesamtabweichung = erklärte Abweichung + nicht erklärte Abweichung | ||||
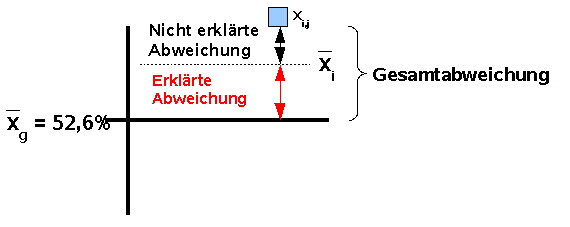 | ||||
Abb. 6: Darstellung Streuungszerlegung | ||||
Dieser Ansatz der Gesamtabweichung (Streuungszerlegung) wird zur Ermittlung der Abweichungsquadrate (siehe auch Schwerpunkteigenschaft) nach folgenden Formeln genutzt: |
| |||||||||||||||||||||||||||||||||||||||||
Folgende Tabelle (Abb. 7) zeigt die Abweichungsquadrate für unser Beispiel aus Abb. 5: |
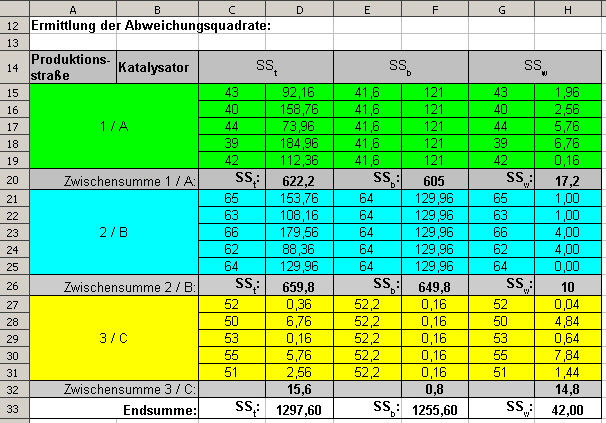 |
Abb. 7: Abweichungsquadrate für Beispiel einfaktorielle Varianzanalyse |
Die Quadratsumme der Abweichungen stellt ein Maß für die Streuung dar. Es ist ersichtlich, dass die Größe der Quadratsumme von der Anzahl der Beobachtungen abhängig ist. Um die Streuung unabhängig von der Anzahl Beobachtungen (Werte) zu machen, wird sie durch die Anzahl Beobachtungen -1 ( n-1, Freiheitsgrad) dividiert. Damit erhalten wir die mittlere quadratische Abweichung (mean sum of squares, Varianz s): |
|
|
Bevor die Varianzen berechnet werden können, müssen die Freiheitsgrade
df für die summierte Abweichungsquadrate ermittelt werden. |
| ||||||||||||||||||||||||||||||||||||
 |
Abb. 8: Varianzen der Abweichungen |
Ausgehend von der Streuungszerlegung nehmen wir an, dass SSb durch die unabhängige Variable und SSw durch nicht erfasste, zufällige Einflussgrößen bestimmt wird. Das bedeutet für unser Beispiel, da Sssb deutlich größer als Sssw, der Katalysator einen erheblichen Einfluss auf das Isomerenverhältnis hat. |
|
Oder allgemein formuliert, je größer die Varianz Sssb im Vergleich zur Varianz Sssw ist, desto eher ist ein Einfluss der unabhängigen Variablen anzunehmen. Die Wirkung der unabhängigen Variablen auf die abhängige Variable wurde schon grafisch in Abbildung 6 dargestellt. Formalisiert entspricht dies für die einfaktorielle Varaianzanalyse folgendem Modell: x(i,j) = x(i,j): Ausprägung des abhängigen Merkmals
|
|
| ||||||||||||||||
Die Prüfgröße PG wird mit dem F-Wert der theoretischen F-Verteilung verglichen. |
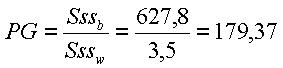 | |||
F12, berechnete PG | |||
... und unsere Nullhypothese H0 lautet, dass kein Unterschied zwischen den verschiedenen Katalysatoren (Faktorenstufen, Produktionsstrassen) besteht: H0 = a1 = a2 = a3 = 0 Die Alternativhypothese H1 lautet dann hingegen, dass ein Unterschied zwischen den Katalysatoren besteht: H1 = min. ein a-Wert <> 0 Wenn Sie zur Verdeutlichung noch einmal auf die Spalte Sssb der Abbildung 7 schauen, werden Sie sicher erwarten, dass die Alternativhypothese H1 zutrifft. |
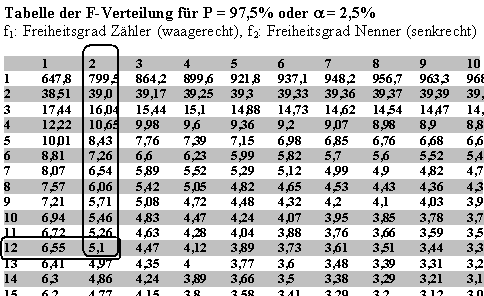 | ||
Abb. 9: Ermittlung des F-Wertes | ||
f1, Freiheitsgrad Zähler, entspricht dem Freiheitsgrad df Sssb und f2, Freiheitsgrad Nenner, dem Freiheitsgrad Sssw. Der Wert der F-Verteilung entspricht somit: F-Wert(2,12,P=97,5%) = 5,1 |
H0 trifft nicht zu, wenn PG > F-Wert |
Für unser Beispiel trifft H0 nicht zu, weil PG > F-Wert(2,12,P=97,5%) 179,37 > 5,1 Die Alternativhypothese H1 muss aufgrund des obigen Vergleichs angenommen werden. Somit liegt mit einer Wahrscheinlichkeit von 97,5% ein Wirkeinfluss der Katalysatoren vor. Beispiel zweifaktorielle Varianzanalyse Die Erweiterung der einfaktoriellen Varianzanalyse auf die zweifaktorielle Varianzanalyse, d. h. die Untersuchung des Einflusses von zwei unabhängigen Merkmalen auf ein abhängiges Merkmal (Abb. 2), wird auch Faktorielles Design genannt. Dabei wird auf das Prinzip der einfaktoriellen Varianzanalyse aufgebaut. Die einfaktorielle wird dadurch auf die zweifaktorielle Varianzanalyse erweitert. Durch 3 Katalysator- und 2 pH-Wert-Varianten ergeben sich 3 * 2 Kombinationen der Faktorenstufen (Katalysator * pH-Wert) und diese 3x2-Matrix führt zur gebräuchlichen Bezeichnung 3x2-faktorielles Design. Die Stichprobenzahl (Zahl der Experimente) erhöht sich dadurch notwendigerweise auf 3 * 2= 6. |
|
| ||||||||||||||||
Eine einfache Prüfung auf Wechselwirkungen zwischen den Merkmalen (Faktoren) kann über eine grafische Darstellung der Faktorenstufenmittelwerte (Isomer I) erfolgen. Abb. 11 zeigt die Faktorenstufenmittelwerte... |
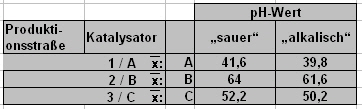 | ||
Abb. 11: Faktorenstufenmittelwert | ||
... und Abb. 12 zeigt die grafische Darstellung: |
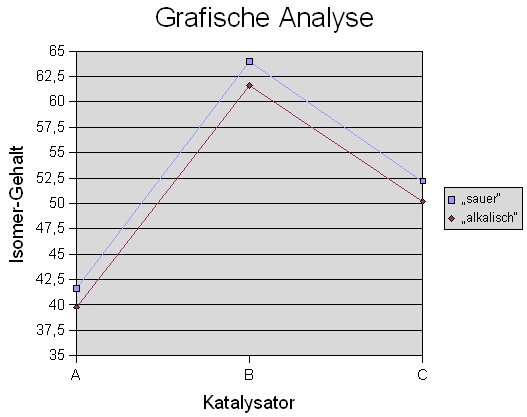 | |||
Abb. 12: Grafische Prüfung auf Wechselwirkung | |||
Es liegt keine Wechselwirkung vor, wenn die Verbindungslinien zwischen den Merkmalmittelwerten aus Abb. 10 oder Abb. 11 wie in Abb. 12 gezeigt, nahezu parallel verlaufen. Hier ist natürlich Ihre Interpretationsfähigkeit verlangt. Denn zwischen nahezu und nicht parallel müssen Sie interpretieren, da ein nichtparalleler Verlauf auf eine Wechselwirkung zwischen den Merkmalen (Faktoren) hinweist. |
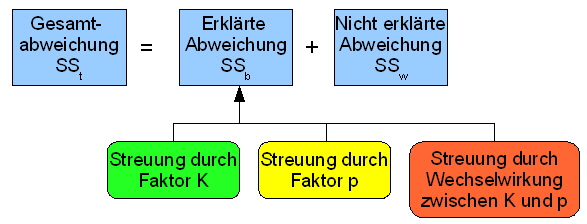 | |
Abb. 13: Übersicht Streuungszerlegung | |
Aus der vereinfachten Darstellung SSt = SSb + SSw (hellblaue Kästchen) wird SSt = SSK + SSp + SSK*p + SSw F13 in der SSb durch die Streuungen des Faktors K (SSK), des Faktors p (SSp)und der Wechselwirkung zwischen den Faktoren K und p (SSK*p) ersetzt
wurde (F13). x(i,j,k) = x(i,j,k): Ausprägung des unabhängigen Merkmals
Zur übersichtlichen Berechnung der Abweichungsquadrate wird die Tabelle aus Abb. 10 um die nötigen Summenstufen und um die Berechung der Zeilenmittelwerte |
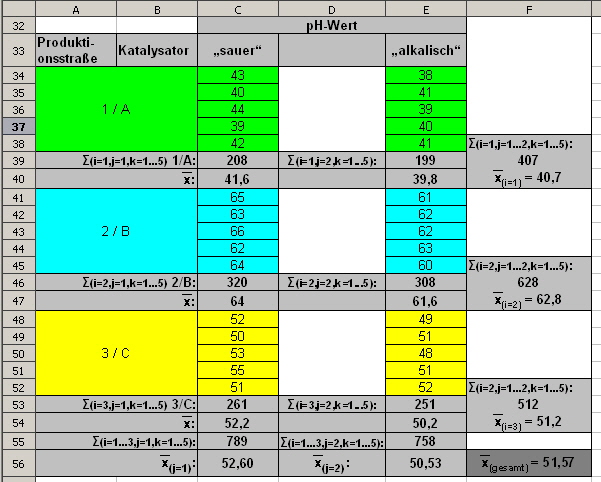 |
Abb. 14: Bespieldatensatz erweitert um die Summenstufen |
|
In den Differenzen der Mittelwerte
Analog der einfaktoriellen Varianzanalyse wird der Einfluss der Faktoren auf die Gesamtstreuung SSt geprüft (siehe F13). |
|
|
.... und beträgt SSt = 2541,37
. Die Hauptbeeinflussung (Haupteffekte, main effects) erfolgt (... sollte erfolgen ...) durch die Faktoren K(atalysator) und p(H-Wert) und werden, wie schon angedeutet, über die Abweichung der Zeilen- bzw. Spaltenmittelwerte ( |
|
|
| ||||||||||||||||||||
Und für unser Beispiel auf Basis von Abbildung 14 beträgt SSK = 2*5[(40,7-51,57)2+(62,8-51,57)2+(51,2-51,57)2] = 2444,07 und SSp = 3*5[(52,6-51,57)2+(50,53-51,57)2] = 32,14 Die Wechselwirkung zwischen den Faktoren “Katalysator” und “pH-Wert” wird wie folgt geschätzt: |
|
|
|
Der Schätzwert x*ij ist der Mittelwert der als Mittelwert
x*ij = Die Abweichung zwischen beobachtetem Mittelwert (siehe Abb. 14) z.B. für Katalysator A und pH-Wert “sauer” SSK*p = 5[(41,6-41,73)2+(39,8-39,66)2+(64-63,83)2+(61,6-61,76)2+(52,2-52,23)2 Jetzt sind wir in der Lage, den SSb-Wert zu berechnen. Wir wissen, dass der SSb-Wert zusammen gesetzt wird aus der Streuung des Faktors K (SSK), des Faktors p (SSp) und der Wechselwirkung der Faktoren K und p (SSK*p). Somit lässt sich SSb berechnen: SSb = SSK + SSp + SSK*p F19, siehe auch F13 SSb = 2444,07 + 32,14 + 0,47 = 2476,68 Als letzter Schritt der Berechnung der summierten Abweichungsquadrate wird die “nicht erklärte”, die zufällige Streuung SSw geschätzt. |
|
|
Hier bemühen wir wieder das Tabellenkalkulationsprogramm, um die Berechnung auf Basis von F20 übersichtlicher zu gestalten (Abb. 16): |
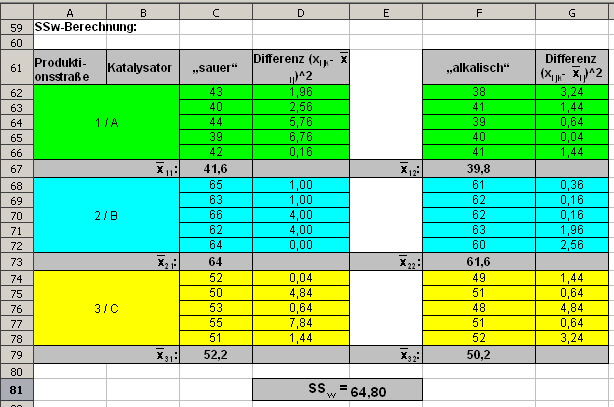 |
Abb. 16, Berechnung von SSw |
Der SSw-Wert beträgt 64,8. Die obige Schätzung nach F20 wäre nicht nötig zur Ermittlung des SSw-Wertes gewesen, da mit SSt und SSb auf Basis von F13 bzw. der Streuungszerlegung SSw die Differenz as SSt und SSb ist. Die Berechnung über diesen Weg sollten Sie aus Kontrollgründen durchführen, nur denken Sie an mögliche Rechenungenauigkeiten. Tragen wir die Werte der Streuung zusammen: SSt = SSb + SSw Oder SSb aufgelöst: SSt = SSK + SSp + SSK*p + SSw In der nach SSb aufgelösten Form, ist natürlich mehr Information enthalten. Sie können den Anteil der Hauptbeeinflussungen durch die Faktoren, hier SSK und SSp, abschätzen. Dadurch können Sie erkennen, dass der Einfluss von SSp (32,14) im Vergleich zu SSK (2444,07) sehr gering ist. Hinzu kommt der bedenkliche Vergleich zwischen SSp und SSw (64,8). Kommen wir zur statistischen Prüfung
auf unterschiedlichen Einfluss der beiden Faktoren. Die Berechnung der SS-Werte erfolgt über die Mittelwerte und darauf formulieren wir unser Hypothesen. Sind alle Mittelwerte gleich, kann angenommen werden, dass keine Beeinflussung der jeweiligen Faktorenstufe (Ausbeute Isomer I) vorliegt (Nullhypothese H0). Die Alternativhypothese H1
liegt dann vor, wenn mindestens ein Faktor Auswirkungen auf die Faktorstufe zeigt. df SSK = i - 1 = 3 - 1 = 2 Aus den SS-Werten und den zugehörigen Freiheitsgraden wird die Varianz berechnet (Abb. 17): |
|
Abb. 17: Tabelle der Varianzen |
Die Prüfgröße PG wird durch Division der Varianzen mit der Varianz der “Nicht erklärten Streuung (w)” (gelbe Zeile, siehe F12) berechnet und neben den tabellarischen F-Werten und Hypothesen tabellarisch dargestellt (Abb.18): |
|
Abb. 18: Prüfung der Hypothesen |
Mit einer Wahrscheinlichkeit P=97,5% zeigen die Faktoren Katalysator und pH-Wert einen Einfluss auf die Faktorenstufe (abhängiges Merkmal). Ebenso liegt mit einer Wahrscheinlichkeit P=97,5% keine Wechselwirkung zwischen den Faktoren Katalysator und pH-Wert vor. Bemerkungen zur Varianzanalyse Die Varianzanalyse ist ein strukturprüfendes Verfahren. Das bedeutet, dass die Frage, die durch die Varianzanalyse beantwortet werden soll, sich nicht erst aus den Daten ergeben darf. Von den Daten des unabhängigen sowie des abhängigen Merkmals
und der Hypothese hängt die inhaltliche Relevanz der Aussage ab. Es wird keine Aussage über die Stärke des Zusammenhangs gemacht. Siehe hierzu auch Abb. 18. |
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |