 |
Kovarianz und Standardabweichung für a,b und r | |||
Bisher wurde der Korrelationskoeffizient r als einziges Kriterium zur Beurteilung der Qualität einer lineraren Funktion beschrieben. Es wird gezeigt, wie weitere Daten zur Genauigkeit, wie die Standardabweichung für a, b, r und die Kovarianz, einer Funktion berechnet (“geschätzt”) werden. Diese Daten “verfeinern” die simple Angabe der Funktionsgleichung und des Korrelationskoeffizienten. Siehe dazu auch das Thema Homoskedastizität! |
 |
|
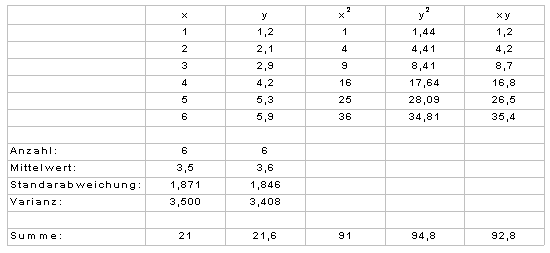
Obige Tabelle (Tabelle 1) dient als Ausgangsbasis für die folgenden Beispiele. Neben den x- und y-Werten sehen Sie weitere Daten. Diese werden in den Beispielberechnungen benötigt. An dieser Stelle sei erwähnt, dass Sie RGP aus OpenOffice Calc oder auch das Statistikprogramm R nutzen können. Sollten Sie R noch nicht kennen, können Sie ich mit Einführung in R in das kostenfreie Statistikprogramm einarbeiten. |
|
| ||||||||||||||||||||||||||||||||
Die Berechnungen zur Korrelations- und Regressionsanalyse basieren, wie schon erwähnt, auf den Beobachtungswerten x und y. Die Größe der Abweichung dieser Werte vom jeweilgen Mittelwert ist ein Maß für den Grad des Miteinandervariierens der Beobachtungen. Die Kovarianz ist das Analogon zur Standardabweichung und wird wie folgt berechnet: |
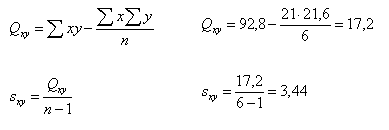 | |||
Korrelationskoeffizient r über die Kovarianz und den Standardabweichungen: | |||
Folgende Berechnung kann als Alternative oder zu Kontrollzwecken gesehen werden: |
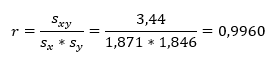 | |||
Regressionskoeffizient b: | |||
Folgende Berechnungen kann als Alternative oder zu Kontrollzwecken gesehen werden: |
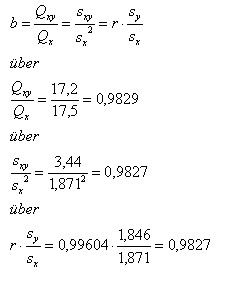 | |||
Die Standardabweichung für y wenn x einen bestimmten Wert auf der Regressionsgeraden annimmt, wird berechnet nach: |
|
|
Die Standardabweichung sy.x kann durch folgende Beziehung geprüft werden: |
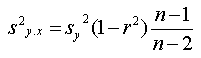 |
Strebt r gegen 0 strebt sy.x gegen sy. Strebt r gegen 1 strebt sy.x gegen 0! |
Die Berechnung erfolgt nach folgender Formel und Beispiel: | |||||||||
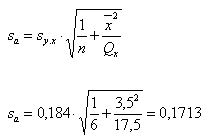 | |||||||||
Standardabweichung sb des Regressionskoeffizienten b: | |||||||||
Die Berechnung erfolgt nach folgender Formel und Beispiel: | |||||||||
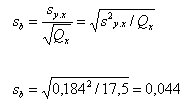 | |||||||||
Sie können die Berechnung von sa und sb wie folgt kontrollieren: | |||||||||
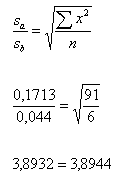 | |||||||||
|
| ||||||||||||||||
Der Vertrauensbereich VB
für die gesamte Regressionsgerade wird über die geschätzte Standardabweichung |
|
|
Obige Rechnung (Schätzung) wird für beliebige x-Werte über den Datenbereich wiederholt: |
|
|
Daraus resultiert eine VB-Matrix über die gewählten x-Werte des Datenbereiches: |
|
Diese VB-Matrix in die graphische Darstellung der Regressionsgrafik übernommen, zeigt dann folgendes beispielhafte Bild (Grafik 3): |
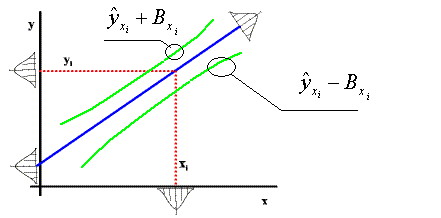 | |||
Grafik 3 | |||
Dabei ist zu berücksichtigen, das die Werte der VB-Matrix zunehmend unsicherer werden, je weiter die Werte von der Mitte der Regressionsgeraden entfernt sind. Graphisch wird dies deutlich, durch die Hyperbeläste in der Darstellung des Vertrauensbereiches (grüne Linien) in Grafik 3. Auf Basis der Daten aus Tabelle 1 wird mit OpenOffice Calc der Vertrauensbereich mit (F2,4,P=97,5%=10,65) geschätzt und graphisch dargestellt (Grafik 4): |
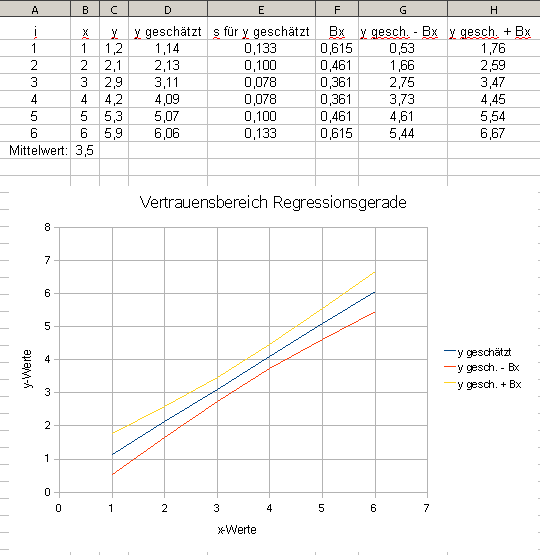 |
Grafik 4 |
Hier können Sie die OpenOffice-Datei aus Grafik 4 laden! | |||
Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen? |