Zurück...

Rangkorrelationskoeffizient

Für zwei abhängige Rangreihen (ordinalskalierte Merkmale) lässt sich über die Rangkorrelation ein monotoner Zusammenhang schätzen. Die Alternativhypothese zu dieser Schätzung ist, dass kein Zusammenhang vorliegt.

Monotoner Zusammenhang bedeutet, dass bei steigender Ausprägung des X-Merkmals die Ausprägung des Y-Merkmals ebenfalls steigt (= positiver Zusammenhang) oder fällt (= negativer Zusammenhang). Siehe zur grafischen Verdeutlichung hier!

  • Schätzung des Rangkorrelationskoeffizienten nach Spearman

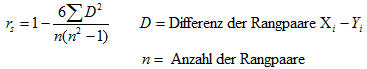Bei dieser Methode wird von der Differenzbildung D zwischen den X- und Y-Rangreihen ausgegangen. Der Rangkorrelationskoeffizient nach Spearman ( (rho), hier aber schlicht rs) wird nach folgender Formel geschätzt:

Eine Übersicht zur Ableitung obiger Formel finden Sie im Bortz. Bei Rängen ist das Thema Bindungen wichtig. Für die Schätzung sollten höchstens 20% der Beobachtungen ranggleich sein (Sachs, Hedderich).
Der Rangkorrelationskoeffizient rs ist in gleicherweise wie der Korrelationskoeffizient mit

interpretierbar.

Spearman-Beispiel mit R:

Folgende ordinalskalierte gepaarten 12 Beobachtungen X und Y sollen auf einen Zusammenhang untersucht werden:

 

1

2

3

4

5

6

7

8

9

10

11

12

X

1

2

3

3

3

3

4

5

6

6

7

8

Y

1

3

2

2

4

4

4

5

6

5

6

7

Die Schätzung des Rangkorrelationskoeffizienten rs wird hier nachvollziehbar dargestellt:

    > X <- c(1,2,3,3,3,4,5,5,6,6,7,8) # Die X-Datenreihe
    > Y <- c(1,3,2,2,4,4,4,5,6,5,6,7) # Die Y-Datenreihe
    # Rang der X-Datenreihe über die R-Funktion rank():
    > Rang.X <- rank(X); Rang.X
         [1]  1.0  2.0  4.0  4.0  4.0  6.0  7.5  7.5  9.5  9.5 11.0 12.0
    # Rang der Y-Datenreihe:
    > Rang.Y <- rank(Y); Rang.Y
         [1]  1.0  4.0  2.5  2.5  6.0  6.0  6.0  8.5 10.5  8.5 10.5 12.0
    # rs nach obiger Formel berechnet:
    > D <- Rang.X - Rang.Y; D  # Bildung der Rangdifferenzen
     [1]  0.0 -2.0  1.5  1.5 -2.0  0.0  1.5 -1.0 -1.0  1.0  0.5  0.0
    > n <- length(D); n  # Anzahl der Werte (Beobachtungen)
         [1] 12
    > rs <- 1-6*sum(D^2)/(n*(n^2-1)); rs
    [1] 0.9370629
    # r über die Funktion cor() (Korrelationskoeffizient) geschätzt:
    > cor(Rang.X, Rang.Y)
    [1] 0.9356008

 Durch die vorhandenen Bindungen wird der Rangkorrelationskoeffizient nach Spearman  rs = 0,9371 im Vergleich zur Schätzung über die Funktion cor() mit r = 0,9356 leicht überschätzt.

Seitenanfang

Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?

Impressum

Datenschutz