 |
Logistische Regression | |||
Methodisch geh├Ârt die logistische Regression zu den strukturpr├╝fenden Verfahren und hat eine verwandtschaftliche Beziehung zur Diskriminanzanalyse und nat├╝rlich zur Regressionsanalyse. Kann die Zielgr├Â├če Y (abh├Ąngige Variable) nur eine bin├Ąre (dichotome Verteilung) oder allgemein eine diskrete Auspr├Ągung, z. B. yi = 1 (f├╝r Erfolg oder wahr oder ...) oder annehmen, kann die unter lineare Regression dargestellte Methode nicht angewendet werden. Dieser Regressionsansatz w├╝rde Werte f├╝r die abh├Ąngige Variable (Zielgr├Â├če) yi < 0 und yi > 1 erlauben. Hier kommt das Verfahren der logistischen Regression zur Anwendung. ├ťber die logistische Regression wird gesch├Ątzt, mit welcher Erfolgswahrscheinlichkeit P ein Ereignis Y, das Eintreten von Erfolg oder Misserfolg, von der/den unabh├Ąngige(n) Variablen X1 und X2 (oder allgemein von X1, ..., Xn) abh├Ąngt. Der Modellansatz nach P = a + bx beinhaltet die Herausforderung, dass die Wahrscheinlichkeit P, wie bekannt, nur zwischen 0 <= P <= 1 liegen kann. ├ťber die logistische Transformation (F1) werden die Funktionswerte auf diesen Bereich begrenzt: |
|
| ||||||||||||||||||||||||||||
Ist die Wahrscheinlichkeit P = 0,5, hat das Merkmal X keinen Einfluss auf die Erfolgswahrscheinlichkeit des Ereignisses Y. D. h., ob das Ereignis Y auftritt oder nicht, h├Ąngt nicht von X ab! Die folgende Grafik beschreibt diese Aussage: |
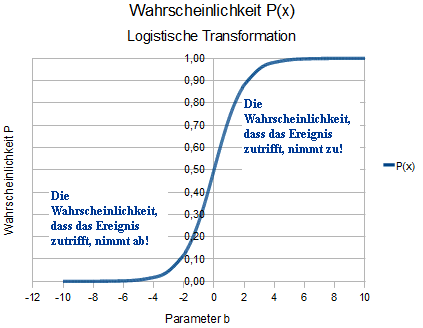 |
├ťber die logistische Transformation kann der obige Modellansatz linearisiert werden (Linkfunktion Logit): log(P(x)) = a + bx Die Sch├Ątzung der Parameter a und b erfolgt nach der Maximum-Likelihood-Methode. Um den rechnerischen Aufwand gering zu halten, wird allerdings das Statistikprogramm R zur Sch├Ątzung bem├╝ht. Zur Sch├Ątzung der Parameter a und b wird die Funktion glm() (GLM: Generalisierte lineare Modelle) mit exponentielle Verteilungsmodelle verwendet. |
|
|
Nun sch├Ątzen wir ├╝ber die Funktion glm() die Parameter a und b und legen das gesch├Ątzte Modell im R-Objekt Ergebnis ab: > Ergebnis <- glm(Zustand ~ Temp, family = binomial("logit")) Unter family wird das exponentielle Verteilungsmodell Binomial und logit (Linkfunktion) angegeben. ├╝ber die Funktion coef() lassen wir uns die Parameter a (= Intercept) und b (= Temp) ausgeben: > coef(Ergebnis) ├ťber beide Parameter l├Ąsst sich durch Einsetzen in F1 die Eintrittswahrscheinlichkeit sch├Ątzen, ob die Gummidichtung bei z. B. -0,6 Grad Celsius (= 31 Grad Fahrenheit) ihre Bestimmung aufgibt, also undicht wird: |
Nach diesem Modell liegt die Ausfallwahrscheinlichkeit der Gummidichtung bei 99,96%! |
Eine Kenngr├Â├čenzusammenfassung erhalten Sie ├╝ber die R-Funktion summary(): > summary(Ergebnis) |
Auff├Ąllig sind die Kenngr├Â├čen zu Deviance Residuals (Deviance: Abweichung, frz. “d├ęvier”) und zu den Koeffizienten (Coefficients), hier der Standardfehler (Std. Error)! Das gesch├Ątzte Modell haben wir im R-Objekt Ergebnis abgelegt. Darauf basierend k├Ânnen wir eine Prognose hinsichtlich der Zielgr├Â├če Y, also der Eintrittwahrscheinlichkeit in Bezug einer bestimmten Temperatur, durchf├╝hren. Dazu werden wir die R-Funktion predict() verwenden. Zuerst legen wir einen Datensatz ├╝ber die Vorhersagetemperatur an: > T.min = 20 #
Grad Fahrenheit Nun wird die Prognose ├╝ber die Funktion predict() durchgef├╝hrt: > Temp.Prognose <- predict(Ergebnis, Temp.Modell, type = "response") Hinweis zum Funktionsaufruf: Da wir glm-R-Objekte nutzen, m├╝ssen wir den type = “response” als predict-Attribut mitgeben (siehe predict.glm)! Lassen wir uns die Prognosetemperatur Temp.Prognose (d. h. die Wahrscheinlichkeiten P) gegen die Vorgabetemperatur Temp.X grafisch darstellen: > sunflowerplot(Temp, Zustand, main = "Darstellung der Prognose", xlab = "Temperatur", ylab = "Wahrscheinlichkeit P") | |||
 | |||
Obige Grafik zeigt, je tiefer die Temperatur desto h├Âher die Eintrittswahrscheinlichkeit, dass der Dichtungsring undicht wird. |
Hat der Inhalt Ihnen weitergeholfen und Sie m├Âchten diese Seiten unterst├╝tzen? |