Zurück...

Weibullverteilung (Zuverlässigkeit-, Lebensdaueruntersuchungen)

Zuverlässigkeitsprüfungen (Lebensdaueruntersuchungen) sind unter Umständen sehr zeitaufwendige Untersuchungen, aber als Qualitätsmerkmal für Produzenten und Kunden wichtige Produktmerkmale.
Auch oder gerade Versicherungsunternehmen führen zur Risikobewertung Lebensdaueruntersuchungen durch und erstellen sogenannte Sterbetafeln.

Zum Einstieg in die Weibullverteilung wird ein Szenario aus dem produzierenden Gewerbe gewählt.
Im Rahmen einer  Zuverlässigkeitsprüfung werden auf Basis einer bestimmten Anzahl Produkte die Ausfälle z. B. über die Zeit ermittelt und geeignet klassiert dargestellt. Es können natürlich auch Anstelle der Zeit andere Parameter, wie z. B. für Motoren die km-Laufleistung, zur Zuverlässigkeitsprüfung herangezogen werden.

Szenario:
Die Zuverlässigkeitsprüfung für einen neuen Typ H7-Halogenscheinwerferlampe ergab folgende klassierte Daten:

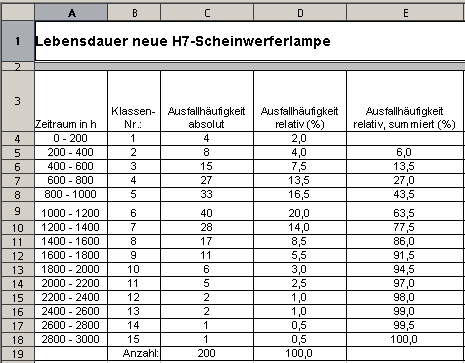Die grafische Darstellung der absoluten Ausfallhäufigkeit als Histogramm, zeigt auch eine deutliche Abweichung von der Normalverteilung:

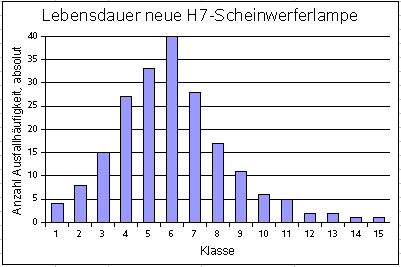Bevor das Szenario fortgesetzt wird, ist nun der Punkt erreicht, wo wir endlich zur Weibull-Verteilung kommen:

Oft lassen sich Lebensdauerverteilungen ausreichend genau durch die nach dem Schweden Waloddi Weibull benannte Verteilung beschreiben. Die Weibull-Verteilungsfunktion G(t) beschreibt die Wahrscheinlichkeit, dass die Lebensdauer höchstens gleich t ist und ist von den Parametern T, charakteristische Lebensdauer und b, der Ausfallsteilheit, abhängig.
Da oft Aussagen über die Überlebenswahrscheinlichkeit oder Zuverlässigkeit  R gemacht werden sollen, wird die Weibullverteilung wie folgt angegeben:

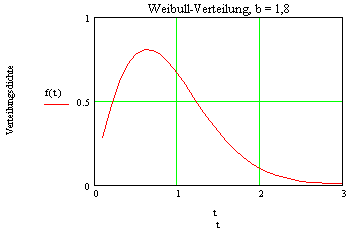
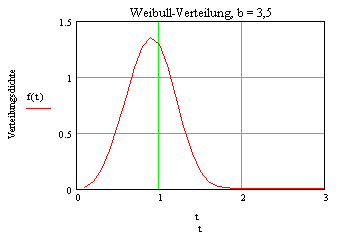
Die folgende Grafikfolge zeigt die Weibullverteilung G(t) in Abhängigkeit von b:

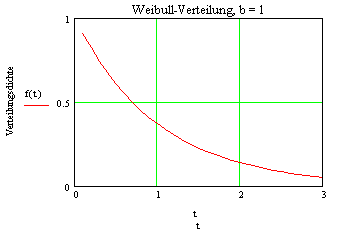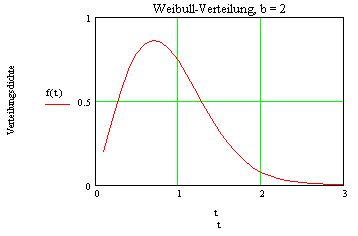Ab einem b-Wert von 3,5 wird die Ähnlichkeit mit der Normalverteilung deutlich.

Hier geht es nun weiter mit dem Szenario: Wie Sie jetzt schon sicher erahnt haben, ist das Problem die Schätzung des Paramters b, die Ausfallsteilheit. Hier sei auf das Thema Korrelation- und Regressionsanalyse, insbesondere lineare Transformation 3. Beispiel, und auf eine Schätzmöglichkeit mit dem Statistiklabor verwiesen. Im Folgenden wird von einem b-Wert = 1,8 (Siehe obige Grafik: Ähnlichkeit Weibullverteilung b = 1,8 und Histogramm!) ausgegangen. Später wird noch gezeigt, dass diese Annahme eine recht gute Näherung ist und auch ohne diverse Algebraprogramme (Mathcad,...) auf Basis von Tabellenkalkulationsprogrammen ermittelt werden kann.
Der Parameter T, die charakteristische Lebensdauer, kann aus obiger Tabelle hingegen direkt geschätzt werden.

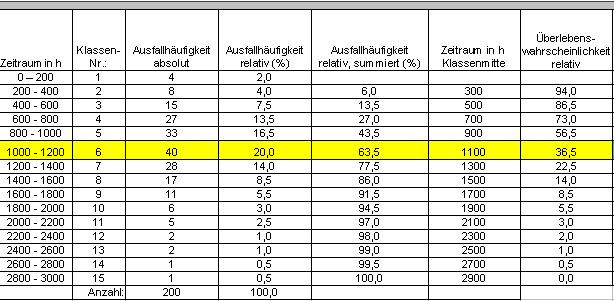
In der Tabelle der klassierten Daten entspricht die Klasse 6 einer relativen Ausfallhäufigkeit von 63,5 % und die Klassenmitte beträgt 1100 h. Der Parameter T wird mit 1100 h angenommen.

Die Ermittlung des Parameters T, bzw. dessen Klasse, kann auch über die Quantilberechnung erfolgen:

Anzahl Werte n = 200, Q soll bei 63 % liegen:

Q_0,63 = (200 + 1) * 0,63 = 126,6

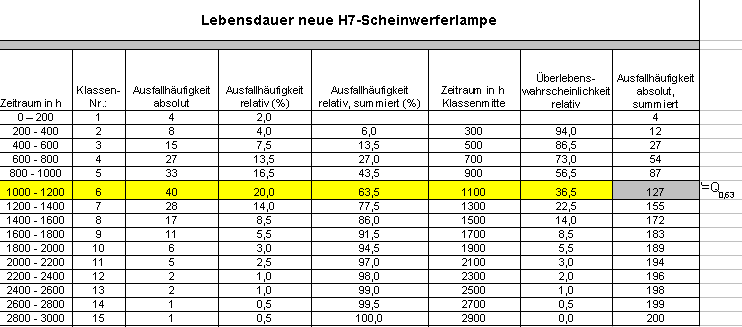
Das Ergebnis 126,6 wird auf 127 aufgerundet. Ca. 63 % Ausfallhäufigkeit werden mit 127 von 200 Lampen erreicht und dies entspricht der Klasse 6 mit der Klassenmitte von 1100 h:

Da nun die Parameter b und T geschätzt wurden, sollte die Validierung der Schätzung erfolgen.
In den Zellen der Spalte H ist obige Formel der Überlebenswahrscheinlichkeit R(t) hinterlegt und die Abweichung der Ergebnisse sind in der Spalte I absolut und in der Spalte J relativ dargestellt:

In Anbetracht der Histogrammform kann von einer recht guten Annäherung ausgegangen werden. Diese Annäherung der Lebensdauerverteilung wird für die weiteren Beispiele genutzt.

Beispiel “Mit welcher Wahrscheinlichkeit wird eine bestimmte Lebensdauer erreicht?”:

Mit welcher Wahrscheinlichkeit R erreichen die H7-Schweinwerferlampen 500 h Betriebsstunden (t)?

T = 1100 h
t = 500 h
R(t) = x

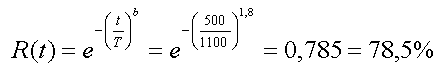Mit einer Wahrscheinlichkeit von R = 78,5 % erreichen die neuen H7-Halogenscheinwerferlampen die Brenndauer von t = 500 h.

Beispiel “Welche Lebensdauer wird mit einer bestimmten Wahrscheinlichkeit erreicht?”:

Welche Brenndauer t wird mit einer Wahrscheinlichkeit von 90 % (R = 0,90) von den H7-Lampen  erreicht? Bevor diese Frage beantwortet werden kann, muss die R(t)-Funktion nach t umgestellt werden:

Zur vorgegebenen 90 %igen Wahrscheinlichkeit R können 315 Betriebsstunden h erwartet werden.

Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?