Zurück...

Lexikon

Sprung zum Bereich:

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z            Literaturstellen       Links

A

ABC-Analyse siehe hier!

Abbildung, Zuordnungsvorschrift für Elemente von Mengen

Absolutbetrag siehe hier!

Abszisse: Bezeichnung für die “horizontale” Koordinate des kartesischen Koordinatensystems (x-Achse).

Abweichung (deviation, error):

Ist die Abweichung zwischen einem Merkmalswert und einem Bezugswert des Merkmals.

Ähnlichkeit und Distanz

AIC (An Information Criterion) siehe hier!

Analysenprobe siehe Messprobe

Analytische Sensitivität (Empfindlichkeit) (analytical sensitivity):

Sie beschreibt die Fähigkeit einer Prüfmethode zwischen z. B. konzentrationsabhängigen Signalen zu differenzieren (Steigung einer Kalibrierfunktion).

Analytische Spezifität (analytical specifity):

Ist die Fähigkeit einer Prüfmethode, nur die gesuchte Substanz zu erfassen, wobei andere Bestandteile der Matrix das Prüfergebnis nicht beeinflussen.

Angepasstes Bestimmtheitsmaß r² (Adjusted r²) siehe hier!

Annahmeprüfung:

Qualitätsprüfung zur Feststellung, ob ein Produkt wie bereitgestellt oder geliefert annehmbar ist.

ANOVA: analysis of variance / Varianzanalyse, mehr dazu hier....!

Anti-Image-Kovarianz-Matrix:

Dient zur Eignungsprüfung einer Korrelationsmatrix in der Faktorenanalyse, mehr dazu hier!

arbitrary origin: willkürlicher Nullpunkt

Assoziativgesetz: (siehe auch Kommutativgesetz)

(a+b)+c = a+(b+c)                     (a*b)*c = a*(b*c)

Audit (Qualitästaudit):

Ein Qualitätsaudit, kurz Audit (lat. audire = (an)hören), ist eine systematische und objektive Untersuchung auf Erfüllung von Qualitätsanforderungen (siehe ISO 9000:2000 ff.).

Das Ziel eines Audits ist

• die Qualitätsfähigkeit des Auditiertens zu bestätigen (Zertifikat)
• und / oder frühzeitig Schwachstellen aufzuzeigen, um Maßnahmen zur Verbesserung zu ergreifen.

Es wird in 3 Auditarten unterschieden:

1. Prozessaudit: Überprüfung der Zweckmäßigkeit und der Einhaltung von Prozessen
2. Systemaudit: Überprüfung des QM-Systems oder von Teilen des QM-Systems
3. Produktaudit: Überprüfung der Übereinstimmung von Produkten mit den festgelegten Qualitätsanforderungen

Und es wird auch danach unterschieden, wer das Audit durchführt:

• Internes Audit: Managementwerkzeug der Unternehmensleitung zur internen Beurteilung und Aufrechterhaltung der Qualitätsfähigkeit.
• Externes Audit: Beurteilung der Qualitätsfähigkeit eines Unternehmens durch eine unternehmensfremde Stelle.

Ausreissertest, siehe Extremwert

Aussage:

Eine Aussage ist ein feststellender Satz, dem eindeutig einer der beiden Wahrheitswerte wahr oder falsch zugeordnet werden kann.

Axiom:

Ein Axiom (Postulat) ist eine Aussage, die von vornherein als wahr vorausgesetzt wird und nicht bewiesen werden kann. Sie stellen das Fundament dar, auf dem mathematische Theorien aufbauen.

Bartlett-Sphärentest findet Verwendung in der Eignungsprüfung der Korrelationsmatrix in der Faktorenanalyse.

Bartlett-Test auf Gleichheit mehrerer Varianzen bei gleichem oder unterschiedlichen Stichprobenumfängen.

Befragung siehe Primär- und Sekundärstatistik

Beobachtung siehe Primär- und Sekundärstatistik

Beschränktheit -

- Funktionen, -Intervalle

Beschreibende Statistik oder gleich deskriptive Statistik...

Bestimmungsgrenze: siehe Nachweisgrenze

Bias:

Als Bias oder auch Verzerrung, wird der systematische Einfluss auf erhobene Daten genannt. Das bedeutet, dass die durchgeführten Schätzungen ein konstantes zu hohes oder zu niedriges Resultat zeigen. Ursachen dieser Verzerrung können sein:

• Die entnommene Stichprobe aus der Grundgesamtheit ist nicht repräsentativ  (Stichprobenumfang zu klein, eine bestimmter Bereich / bestimmte Gruppe wurde bevorzugt, ...)
   
• Wenn in einer Befragung durch nicht optimal formulierte Fragen Antwortoptionen möglich sind, können dadurch Verzerrungen in den Antworten auftreten.
   
• Wird die Datenerhebung mithilfe eines Messinstrumentes durchgeführt, kann dieses dejustiert sein und dadurch systematische verschobene Ergebnisse liefern.
   
• Sind z. B. in einem medizinischem Experiment den Testpersonen oder den Beobachtern (Betreuern) bekannt, wer den Wirkstoff oder ein Placebo bekommen hat, kann dies als Verzerrung in das Ergebnis einfließen.
   
• Werden in der Datenanalyse Daten/Beobachtungen ausgewählt, hat diese Vorgehensweise sicher einen Einfluss auf die Aussage / das Ergebnis. Unter Auswählen wird hier nicht das Aussortieren von ungültigen oder unsinnige Antworten einer Befragung gemeint! Ist eine Datenbereinigung notwendig, wird sie entsprechend dokumentiert! Siehe auch Extremwert.

Big Data, in Verbindung mit Data Mining siehe hier!

Bijektivität, siehe hier!

Bindungen

Hinweise zu Bindungen in Datenerhebungen finden Sie hier!

Binomialverteilung

Blindwert (siehe auch Richtigkeit)

BLUE:

Der Begriff BLUE steht im Zusammenhang mit der Regressionsanalysen und beschreibt die Voraussetzungen, damit die Schätzung der Regressionsanalyse die bestmöglichen Ergebnisse liefert. Unter folgenden Voraussetzungen werden die Koeffizienten der Regressionsanalyse als BLUE (der beste, lineare, unverzerrte und effizienteste Schätzer) bezeichnet:

• Die Regressionsfunktion ist richtig spezifiziert und enthält alle relevanten unabhängigen Variablen.
• Die Abweichungen der beobachteten Y-Werte von den geschätzten Y-Werten haben den Erwartungswert = 0.
• Die Abweichung korreliert nicht mit den unabhängigen Variablen.
• Die Varianz der Abweichungen ist konstant.
• Zwei oder mehrere unabhängige Variablen sind nicht miteinander korreliert.
• Die Abweichungen sind zueinander unkorreliert.
• Die Abweichungen sind normalverteilt.

Unverzerrt bedeutet, dass der Erwartungswert der Koeffizienten den wahren Werten der Koeffizienten der Grundgesamtheit entspricht. Effizient bedeutet, dass die Koeffizienten mit der kleinstmöglichen Streuung geschätzt werden.

Bogenmaß, Beziehung Grad und Bogenmaß (Radiant, rad)

Box-Plot als grafische Zusammenfassung der Quantile

Charge: Begriffe zur Probenahme

Chemometrie:

Chemometrie ist der Teil der chemischen Disziplinen, der mathematische und statistische Methoden zur Auswahl optimaler Messverfahren, zur Plannung von Experimenten und zur Gewinnung maximaler Informationen bei der Analyse der erhaltenen Daten verwendet.

Chiquadrat-Test, -Test:

Der -Test ist ein Anpassungstest. Mit ihm lässt sich prüfen, ob die beobachtete Verteilung der vorgegebenen Verteilung entspricht. Mehr dazu hier...!

Clusteranalyse siehe Multivariate Analysenmethoden

Cohen’s d, Effektstärke:

Über den Cohen’s d kann die Effektstärke für unabhängige Stichproben geschätzt werden. Dieser Test bietet sich im Nachgang zum t-Test  an. Die Prüfgröße d ist die Mittelwertdifferenz der Beobachtungen normiert über die Standardabweichungen:

Zur Interpretation und Vergleichbarkeit führte Cohen diese Einteilung ein:

d = 0,2   geringer / kleiner Effekt
d = 0,5   mittlerer Effekt
d = 0,8   starker / großer Effekt

Ein Beispiel für einen sehr staken Effekt:

Mittelwert₁: 98,133,   Standardabweichung₁: 0,294,  Anzahl Beob.₁: 15
Mittelwert₂: 95,107,   Standardabweichung₁: 0,343,  Anzahl Beob.₁: 15

Conjoint Measurement siehe Multivariate Analysenmethoden

c_p- und c_pk-Index:

Die Prozessfähigkeit wird neben weiteren, durch die Indices c_p, process capability, und durch c_pk, critical process capability, beschrieben. Mehr dazu und die Berechnung finden Sie hier....!

Data Mining:

Eine Übersicht über das Thema Data Mining finden Sie hier und das erwähnte Data-Mining- Projekt-Modell  CRISP-DM 1.0 können Sie über diesen Link auf Ihren Computer laden!

Datenerhebung:

Sind die Daten zur statistischen Betrachtung schon vorhanden, wird von einer Erhebung gesprochen. Es werden folgende Erhebnungsarten unterschieden:

• Primärstatistische Erhebung: Die Daten werden speziell zur Beantwortung einer aktuellen Fragestellung erhoben, z. B. politische Umfragen.
• Sekundärstatistische Erhebung: Bereits vorhandene Originaldaten aus z. B. Datenbanken weren zur Auswertung herangezogen.
• Tertiärstatistische Erhebung: Diese Daten stehen nur noch in transformierter Form, z. B. als Mittelwerte, zur Verfügung.

Diagnosemethoden (Psychologie):

• Querschnittsdiagnose:
  Querschnittsdiagnosen betrachtet den aktuellen Zustand des Objekts, z. B. Unterschiede in den Merkmalsausprägungen zwischen Personen oder Gruppen.
• Längsschnittdiagnose:
  Längsschnittdiagnosen betrachtet Veränderungen über einen größeren Zeitraum des Objekts (Veränderungen von bestimmten Merkmalen von z. B. Personen mit zunehmenden Alter).
   

Diskriminanzanalyse siehe Multivariate Analysenmethoden oder hier...!

Deskriptive Statistik:

Beschreibende Statistik durch graphische Aufbereitung und Komprimierung (z. B. Mittelwert und Streuung) von Daten (siehe auch explorative und induktive Statistik).
Ein Einführungsvideo zur deskriptiven Statistik mit MS Excel finden Sie hier!

Dispersionsmaße:

Maße, die die Variabilität der Verteilung kennzeichnen, wie z. B. Standardabweichung oder Spannweite.

Distanz und Ähnlichkeit

e (Euler’sche Zahl):

Der Grenzwert der Funktion ...

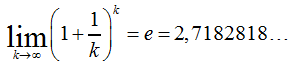... ist die e-Zahl, oder auch nach Leonhard Euler Euler’sche Zahl genannt. Die e-Zahl ist häufig die Basis für Wachstumsprozesse in der Natur und wird deswegen als natürliche Basis bezeichnet. Als Beispiel sei hier das Bakterienwachstum genannt:

Effekte (effects):

Einfach ausgedrückt, sind Effekte für die wir uns interessieren fixed effects (oder auch feste Faktoren) und Faktoren die in unseren Beobachtungen enthalten sind, für die wir uns weniger interessieren, random effects (oder auch Zufallsfaktoren). Die gebildete Hypothese entscheidet letztendlich, was für den Prüfer ein fixed oder random effect ist.

Effektstärke:

- Cohen’s d, siehe hier!

Eichen (verification):

Das Eichen eines Messgerätes umfasst die von der zuständigen Eichbehörde nach den Eich- vorschriften vorzunehmenden Prüfungen und die Stempelung. (DIN 1319 Teil1)

Eingangsprüfung (receiving inspection):

Annahmeprüfung an einem zugelieferten Produkt durch den Abnehmer.

Emperie (empirical):

Die Empirie (griechisch embiría - die Erfahrung) stellt im wissenschaftlichen Sinne eine auf methodischem Weg (Induktion, Analogie, Beobachtung und Versuche) gewonnene Erfahrung dar. Hier wird z. B. unter empirische Verteilung eine Verteilung verstanden, die beobachtete oder durch Versuche gewonnenen Daten basiert.

Endprüfung (final inspection):

Letzte der Qualitätsprüfungen vor Übergabe der Einheit (Lot, Charge) an den Abnehmer.

Entscheidungsbaum oder Regressionsbaum siehe hier!

Ergebnisabweichung (error of result):

Unterschied zwischen einem Merkmalswert und dem Bezugswert, wobei dieser je nach Festlegung oder Vereinbarung der wahre, der richtige oder der Erwartungswert sein kann.          (Siehe Genauigkeit und Wahrer Wert)

Ergebnisraum: (Stichprobenraum, Wertebereich eines Merkmals)

Ein Ergebnisraum stellt die Anzahl möglicher Zufallsergebnisse dar (siehe auch Merkmal und Zufallsvariable).
Für einen Würfel beträgt im Allgemeinen der Ergebnisraum E = {1, 2, ..., 6}und für den Wurf einer Münze beträgt E = {Wappen, Zahl}.
Teilmengen aus z. B. dem “Würfel”-Ergebnisraum heißen Ereignisse, z. B.

Ereignisse E_T = {1, 2, 3}

und einelementige Teilmengen werden als Elementarereignis, wie z. B.

Elementarereignis E_E = {1}

bezeichnet.

Ergebnisunsicherheit (Messunsicherheit):

Geschätzter Betrag zur Kennzeichnung eines Wertebereichs, innerhalb dessen der Bezugswert liegt (siehe Vertrauensbereich für den Mittelwert und Wahrscheinlichkeit).

Erhebungsarten siehe Primär- und Sekundärstatistik

Ermittlungsergebnis (result of determination):

Durch die Anwendung eines Ermittlungsverfahrens (Prüfmethode) festgestellter Merkmalswert (Merkmalsergebnis).

Erstprüfung:

Erste in einer Folge von vorgesehenen oder zugelassenen Qualitätsprüfungen.

Erwartungswert (expectation):

Stellt praktisch den Mittelwert der Merkmalergebnisse, die durch “unablässiges” Wiederholen gewonnen wurden, dar.

Explorative Statistik:

Suche nach Strukturen und Besonderheiten in den Daten (siehe auch deskriptive und induktive Statistik).

Extremwert:

Bei einem Extremwert handelt es sich um auffällig hohe oder kleine Beobachtungen (Messwert...) einer Stichprobe. Hier stellt sich die Frage, ob derartige Beobachtungen als Ausreisser aus der Stichprobe gestrichen werden können. Diese Frage kann mit einem Ausreissertest beantwortet werden.

Experiment siehe Primär- und Sekundärstatistik

Faktorenanalyse siehe Multivariate Analysenmethoden

Faktorielles Desgin ist ein Begriff aus der Varianzanalyse (ANOVA).

Fehler (nonconformance):

Nichterfüllung vorgegebener Forderungen durch ein Merkmalswert. Die Verwendbarkeit ist durch einen Fehler nicht notwendigerweise beeinträchtigt.

Fehlerklassifizerung (classification of...): Einstufung möglicher Fehler einer Einheit in Fehlerklassen nach einer Bewertung, die an die Fehlerfolgen ausgerichtet ist.

Kritischer Fehler (critical ...): Fehler, von dem anzunehmen oder bekannt ist, dass er gefährliche oder unsichere Situationen schafft; oder die Erfüllung der Funktion........ verhindert.

Hauptfehler (major...): Nicht kritischer Fehler, der voraussichtlich zu einem Ausfall führt oder die  Brauchbarkeit für den vorgesehenen Verwendungszweck wesentlich herabsetzt.

Nebenfehler (minor...): Fehler, der voraussichtlich die Brauchbarkeit für den vorgesehenen Verwendungszweck nicht wesentlich herabsetzt, oder den Gebrauch/Betrieb der Einheit nur geringfügig beinflusst.

Fehlerfortpflanzung:

Rechnen mit fehlerbehafteten Zahlen, siehe hier...!

Fehler 1. und 2. Art siehe hier!

Fertigungsprüfung:

Zwischenprüfung an einem in der Fertigung befindlichen materiellem Produkt.

Fischgräten-Diagramm siehe hier!

Fishers exakter Test siehe hier!

FMEA:

FMEA steht für Fehlermöglichkeits- und Einflussanalyse. Mehr zum Thema finden Sie hier!

Formmaße:

Maße, die die Abweichung einer Verteilung von der Normalverteilung charakterisieren, wie z. B. Schiefe- und Wölbungsmaße (Momentkoeffizienten).

Fragebogenkonstruktion, Hinweise zur -:

Die folgenden Hinweise sollen Sie bei der Konstruktion eines Fragebogens zur Datenerhebung unterstützen:

• Seien Sie sich darüber im Klaren, dass die Befragten immer in der Lage sind, Testergebnisse (über die Merkmale einer Erhebung / Befragung) willentlich zu beeinflussen. Das gilt vor allem, wenn sozial erwünschtes Verhalten für den Befragten erkennbar wird.
• Fragen, bei den erwartet wird, dass immer Zustimmung oder Ablehnung erfolgt sollten erst gar nicht gestellt werden.
• Begriffe mit mehreren Bedeutungen vermeiden.
• Verwenden Sie nur von bekannte Begriffe in Fragestellungen. Wenn Sie Zweifel haben, erklären Sie den Begriff!
• Fragen nur einem sachlichen Inhalt zugrunde legen (Vermeidung der Kombination wie z. B. ...sehr gerne und sehr schnell…)
• Keine doppelten Verneinungen
• Keine Verallgemeinerungen
• Die Frage nicht zu lang (Schachtelsätze) aber auch nicht zu kurz (dass das Verständnis verloren geht) formulieren
• Bezieht sich eine Frage auf einen Zeitraum, diesen deutlich definieren (nicht in den letzten Monaten, sondern in den letzten 3 Monaten…)
   
• Wenn möglich, prüfen Sie den Fragebogen durch eine Vorbefragung auf Verständlichkeit (weiter Stichworte sind Validität und Reliabilität).
   
• Vermeiden Fragen vom Ja/Nein-Antwort-Typ
  Dieser Fragetyp ist bei einer exakten und gut verständlichen Fragestellung leicht zu beantworten. Allerdings erhält man zu wenig differenzierte Informationen. Eine Triebkraft für diesen Hinweis ist die Schwierigkeiten bei der statistischen Analyse.

Diese Hinweise sind sicher nicht umfassend, sie sollen Anregungen sein!

Freiheitsgrad (degrees of freedom, df):

Der Freiheitsgrad (df oder f) entspricht dem Stichprobenumfang n minus der Anzahl Parameter p die aus diesem Stichprobenumfang geschätzt wurden:

df = f = n - p

Der Begriff Freiheitsgrad wird an folgendem Beispiel dargelegt. Dazu gehen wir davon aus, das uns  5 Zahlen vorliegen, deren Summe 25 beträgt und der Mittelwert 5 entspricht.
Basierend auf dieser Annahme können wir nun in der folgenden Tabelle 5 Zahlen, die positiv oder negativ sein können, aber - wie erwähnt - als Summe nur 25 ergeben dürfen, eintragen. Starten wir einfach, völlig willkürlich, mit der Zahl 6 in der ersten Zeile:

Auch ist es egal, welche Zahl als 2. Zahl eingetragen wird. Tragen wir einfach die 4 ein:

Die 3. Zahl kann von uns auch willkürlich gewählt werden, hier die 7:

Und ebenso die 4. Zahl, beispielsweise tragen wir hier eine 3 ein:

Und nun kommen wir zur letzten Zahl! Hier haben wir keine Wahlfreiheit mehr! Um die Summe 25 und folglich einen Mittelwert 5 zu erhalten, müssen wir als letzte Zahl 5 eintragen:

Für die Zahlen 1 bis 4 haben wir völlige Wahlfreiheit aber durch die Vorgabe des Mittelwerts 5 in diesem Beispiel, haben wir keine Wahlfreiheit für die 5. Ziffer mehr. In diesem Beispiel haben wir also nur 4 Freiheitsgerade!

Funktionen, mathematisch betrachtet.

Gauß’sche Zahlenebene

Genauigkeit (accuracy):

Die Genauigkeit ist die Bezeichnung für das Ausmaß der Annäherung von Merkmals- ergebnissen an den Bezugswert, wobei dieser je nach Festlegung oder Vereinbarung der richtige oder ein festgelegter Wert sein kann.

Die Genauigkeit ist der Oberbegriff für Präzision und Richtigkeit.

Gesamtabweichung (total deviation, total error):

Ist die Differenz von Sollwert und Istwert und setzt sich zusammen aus systematischer und zufälliger Abweichung.

Gini-Koeffizient als Abweichungsmaß in der Lorenzkurve

GLM (Generalisierte Lineare Modelle):

GLM ist eine Analyse-Methode aus dem Bereich der Regressionsanalyse. Besonders ist hierbei, dass die abhängige Variable Y (Zielgröße) einen diskreten Charakter, wie z. B. ja = 1 oder nein = 0, hat (siehe auch Skalen). Ein Anwendungsbespiel dieser Methode finden Sie hier!

Grenz-

Grenzbetrag (upper limit amount): Betrag für Mindestwert und Höchswert, die bis auf das Vorzeichen übereinstimmen.

Grenzabweichung (limiting deviation): Untere Grenzabweichung oder obere Grenzabweichung.

Untere Grenzabweichung (lower limiting deviation): Mindestwert minus Bezugswert, wobei der Bezugswert der Nennwert oder Sollwert ist.

Obere Grenzabweichung (upper limiting deviation): Höchstwert minus Bezugswert.

Grenzwert

Griechisches Alphabet

Grundgesamtheit (Population):

Die Grundgesamtheit ist die Gesamtheit aller Merkmalsträger, oder anders ausgdrückt, ist die Menge aller statistischen Einheiten (Objekte, Elemente), über die eine Aussage getroffen werden soll.
Eine Grundgesamtheit kann endlich, unendlich oder hypothetisch sein. Die Grundgesamtheit muss z. B. nach folgenden Kriterien definiert werden:

• Sachlich, was soll untersucht werden?
• Räumlich, wo soll die Untersuchung durchgeführt werden?
• Zeitraum, wann soll die Untersuchung stattfinden?

Wird eine Teilmenge der Grundgesamtheit betrachtet, also darauf beschränkt, wird von einer Teilgesamtheit (Teilpopulation) gesprochen.

Nehmen wir als Beispiel eine Befragung zum nächsten Bundeskanzler als Wahlergebnis der Wahl vom 27. September 2009. Die Befragung wird im gesamten Bundesgebiet (räumlich) in der 4. Wochen vor dem Wahltermin für den Zeitraum von einem Tag an 1008 zufällig ausgewählten Bundesbürger (sachlich, Stichprobe = Teilerhebung) durchgeführt. Das Ergebnis der Umfrage soll eine Aussage (Wahrscheinlichkeitsaussage) sein, wer nächster Bundeskanzler oder natürlich Bundeskanzlerin wird.
Über das Ergebnis dieser Teilerhebung wird auf das Wahlverhalten der Grundgesamtheit (die Gesamtbevölkerung der Bundesrepublik) geschlossen. Deswegen muss die Stichprobe repräsentativ sein. Nicht repräsentativ wäre sicher eine Teilerhebung in nur einem Bundesland. Siehe dazu auch Bias!

Gauß’sche Summenformel

H-Test von Kruskal und Wallis siehe hier!

Häufigkeit, kumuliert (Summenhäufigkeit) siehe hier!

Hauptkomponentenanalyse, methodisch und mit R finden siehe hier!

Histogramm:

Über ein Histogramm lassen sich Häufigkeitsverteilungen grafisch darstellen. Wie ein Histogramm konstruiert wird, sehen Sie hier!

Homoskedastizität (Varianzhomogenität) / Heteroskedastizität

spielt insbesondere im lineare Regressionsmodell eine Rolle. Im linearen Modell

y = a + bx + e

wird davon ausgegangen, dass die Varianz der Residuen e eine konstante Größe und unabhängig von der Ausprägung (dem Wert) der unabhängigen Variable x ist.

Ein Test auf Heteroskedastizität ist z. B. der Breusch-Pagan-Test (bptest() in R).   

Hypergeometrische Verteilung

Hypothese, Null- und Alternativ-:

Eine ausführlichere Beschreibung des Themas finden Sie hier oder hier als Video !

Durch ein statistisches Testverfahren soll z. B. geprüft werden, ob die Länge der produzierten Schrauben einer laufenden Produktion dem Sollwert = 50 mm entsprechen oder ob beispielsweise zwei Stichprobenmittelwerte innerhalb einer zufälligen Schwankung gleich sind (der gleichen Grundgesamtheit entstammen).

Dazu werden Hypothesen formuliert:  Die Nullhypothese H₀ bedeutet, dass nichts geschieht (einfach ausgedrückt) und die Alternativhypothese H₁, dass ein bestimmtes oder extremes Ereignis eingetreten ist. Wichtig ist, dass die Nullhypothese H₀ nicht durch Tests bewiesen wird, sondern dass aufgrund der Beobachtungen und Test gezeigt wird, dass die Nullhypothese H₀ hinreichend unwahrscheinlich ist! Dann wird zugunsten der Alternativhypothese H₁ die Nullhypothese H₀ verworfen.

Was bedeutet das für obige Beispiele? Zeigt der statistische Test, dass der Sollwert von 50 mm Schraubenlänge innerhalb der normalen statistischen Varianz erreicht wird, ist die Wahrscheinlichkeit hoch, dass die Nullhypothese H₀ zutrifft. Zeigt der Test aufgrund der Beobachtungen (deutliche Abweichung der Schraubenlänge von 50 mm) hingegen, dass die Nullhypothese H₀ hinreichend unwahrscheinlich ist, muss sie zu Gunsten der Alternativhypothese H₁ zurückgewiesen werden.
Für das 2. Beispiel bedeutet die Nullhypothese H₀, dass die beiden Mittelwerte innerhalb der normalen statistischen Varianz gleich sind (nichts geschieht). Zeigt ein statistischer Test für den Vergleich der Mittelwerte hingegen einen signifikanten Unterschied zwischen den Mittelwerten, ist die Nullhypothese H₀ zu Gunsten der Alternativhypothese H₁ zurückzuweisen.

Für Hypothesentests werden zur Entscheidung die entsprechenden tabellierten Verteilungen herangezogen oder durch Statistikprogramme wie z. B. R, p-Werte zur Wahrscheinlichkeitsabschätzung berechnet.

Ein Fehler 1. Art tritt nun dann auf, wenn H₀ verworfen wird, obwohl H₀ wahr ist. Und der Fehler 2. Art tritt dann ein, wenn H₀ beibehalten wird, obwohl H₁ wahr ist.

Induktion, Bewies durch vollständige -:

Bei der vollständigen Induktion handelt es sich um eine mathematische Beweismethode, nach der eine Aussage A  für alle natürlichen Zahlen N bewiesen wird:
 

Wenn aus der Annahme, A(n) sei für ein beliebiges n wahr, folgt, dass A(n + 1)wahr ist, und A(1) ebenso eine wahre Aussage ist, gilt

Der Beweis besteht immer aus folgenden Schritten:

• Mit dem Induktionsanfang A(1) wird bewiesen, dass die Aussage für die kleinste Zahl, den Startwert, gilt.
• Mit dem Induktionsschritt wird gezeigt, dass aus der Gültigkeit von A(n) die Gültigkeit von A(n + 1) folgt.

Induktive Statistik:

Versuch durch Einbindung der Stochastik über die erhobenen/ermittelten Daten hinaus allgemeine Schlußfolgerungen für umfassendere Grundgesamtheiten zu ziehen (schließende Statistik, siehe auch deskriptive und explorative Statistik).
Induktiv: Bezeichnet die Vorgehensweise in der Logik des Schließens “vom Besonderen auf das Allgemeine”.

Injektivität, siehe hier!

Interquartilbereich (interquartilrange, IQR):

Der Interquartilbereich kann als Kennzahl für die Verteilung dienen, d. h., die Größe des Bereichs gibt Auskunft, wie weit die Verteilung auseinander gezogen ist.
Die Berechnung des Interquartilbereichs d_Q erfolgt nach

d_Q = Q₃ - Q₁

Der Interquartilbereich ist, da links von Q₁ und rechts von Q₃ die Werte nicht berücksichtigt werden, gegen Extremwerte (Ausreißer) stabil. Als Ausreißer-Kandidaten können Werte vermutet werden, die folgende Grenzen überschreiten:

Unterer Grenzwert = Q₁ - 1,5 d_Q

Oberer Grenzwert = Q₃ + 1,5 d_Q

(EN) ISO 9001:2000 ff, QM-System

(EN) ISO 19011, Leitfaden für das Auditieren von Qualitäts- und /oder Umweltmanagementsystemen

Istwert:

Momentanes Merkmalsergebnis, welches sich durch systematische und /oder zufällige Abweichungen vom wahren/richtigen Wert unterscheidet.

Intervalle:

Ein Intervall stellt eine zusammenhängende Teilmenge einer geordneten Menge dar. Das bedeutet, wenn 2 Objekte in der Teilmenge enthalten sind, sind auch die dazwischen liegenden Objekte in dieser Teilmenge enthalten.
Ein Intervall ist durch seine Intervallgrenzen eindeutig bestimmt. Ein Intervall heißt abgeschlossen, wenn es beide Grenzen enthält und offen, wenn es beide Grenzen nicht enthält. Als halboffen wird ein Intervall bezeichnet, wenn es eine Intervallgrenze beinhaltet:

• Abgeschlossenes Intervall (geschlossen, kompakt):
  
  [1, 10] -> Das Intervall enthält auch die Zahl 1 und 10.
   
• Offenes Intervall (beschränktes):
  
  (1, 10) -> Das Intervall enthält nicht die Zahlen 1 und 10, aber natürlich die Zahlen zwischen 1 und 10. Für die folgenden halboffenen Intervalle gilt dies analog. Eine alternative Schreibweise ist ]1, 10[.
   
• Halboffenes (linksoffenes) Intervall:
  
  (1, 10] -> Das Intervall enthält nicht die Zahl 1 aber die Zahl 10.
   
• Halboffenes (rechtsoffenes) Intervall:
   
• [1, 10) -> Das Intervall enthält die Zahl 1 aber nicht die Zahl 10.

Um Verwechselungen mit dem Dezimalkomma zu vermeiden, werden oft folgende Schreibweisen genutzt:

[1, 10] = [1; 10] = [1 | 10]

Die oben gezeigten Beispiel-Intervalle sind endlich und die größte untere Schranke heißt Infimum und die kleinste obere Schranke Supremum. Neben den endlichen gibt es natürlich auch unendliche  Intervalle, z. B.:

[0,  ] -> Die kleinste Zahl ist 0 und das Intervall ist unendlich lang im Zahlenraum >= 0.

Ishikawa-Diagramm siehe hier!

Julia, Die Programmiersprache -

Junktoren, siehe hier!

Justieren (adjustment):

Justieren bedeutet, ein Messgerät so einzustellen oder abzugleichen, dass die Messabweichungen möglichst klein werden oder dass die Beträge der Messabweichungen die Fehlergrenze nicht überschreiten. (DIN 1319 Teil 1)

Kalibrieren (calibration):

Das Kalibrieren eines Systems ist die Ermittlung und Festlegung eines funktionalen Zusammenhangs zwischen einer zähl- bzw. messbaren Größe und einer bestimmenden Konzentration (Objekteigenschaft) aus Daten, die im allgemeinen mit zufälligen Abweichungen behaftet sind. (DIN 1319 Teil 1)

Kardinalzahlen sind Mengen, die als Repräsentanten von Mengen einer bestimmten Größe dienen (Anzahl, siehe auch Skalen).

Kartesische Produktmenge, siehe hier!

Klassierung (Kategorisierung) von Merkmalsausprägungen siehe hier!

Kommunalitätsproblem als Aspekt der Faktorenanalyse siehe hier!

Kommutativgesetz: (siehe auch Assoziativgesetz)

a+b = b+ a                 a*b = b* a

KMO-Kriterium, Kaiser-Meyer-Olkin-Kriterium

Eignungsprüfverfahren in der Faktorenanalyse, siehe hier!

Kolmogorov-Smirnov-Test (Kolgoroff-Smirnoff-Test) als Anpassungstest zur Prüfung auf Normalverteilung siehe hier!

Konfidenzbereich /-intervall (confidence interval): siehe Vertrauensbereich

Kontingenz- oder Kreuztabelle und Kontigenzanalyse, oder Übersicht der Multivariaten Analysenmethoden

Kontingenzkoeffizienten K*, Kontigenzanalyse, Stärke des Zusammenhangs...

Korrelation (correlation):

Allgemeine Bezeichung für den stochastischen Zusammenhang zwischen zwei oder mehreren Zufallsgrößen.

Im engeren Sinn wird mit “Korrelation” der lineare stochastischen Zusammenhang bezeichnet.

Sind die Beobachtungen vom metrischen Skalentyp, wird der Korrelationskoeffizient nach Pearson geschätzt und sind sie mindestens vom ordinalen Skalentyp, nach Spearman (Rangkorrelationskoeffizient).

Über den t-Test für den Korrelationskoeffizienten, können Sie die Güte des vermuteten statistischen Zusammenhanges zwischen den Merkmalen prüfen. Weiters dazu hier!

Korrelationsmatrix, Inverse -, siehe hier!

Korrespondenzanalyse siehe Multivariate Analysenmethoden

Kreisprozess:

Um auf Fragestellungen Antworten (Resultate) zu finden, hilft der statistische Kreisprozess weiter. Auf Basis der Fragestellung werden die geplanten Daten erhoben, Annahmen über das Modell gemacht, die Daten analysiert und interpretiert. Zeigen Fragestellung und Resultate keinen “inneren” Zusammenhang (Modell / Interpretation) müssen Anpassungen vorgenommen werden, bis dass Modell die Realität befriedigend abbildet.

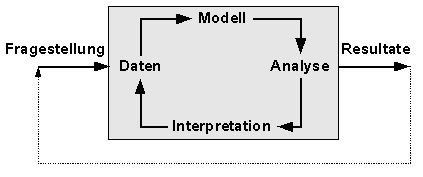Kruskal und Wallis-Test (oder H-Test) siehe hier!

Laplace-Wahrscheinlichkeit siehe hier!

Lebensdaueruntersuchung:

Zum Thema Lebensdaueruntersuchung (Zuverlässigkeits-) siehe Weibullverteilung!

Likert-Skala (nach Renisis Likert), siehe hier!

Logistische Regression , siehe hier!

Logische Verknüpfung, siehe hier!

Logit:

Begiff aus der logistischen Regression, siehe hier!

Lokalisationsmaße:

Maße für die mittlere Lage einer Verteilung, wie z. B. der Mittelwert.

Lorenzkurve als garphische Darstellung der relativen Merkmalkonzentration.

Los: Begriffe zur Probenahme

Matrix, mathematisch -

Matrix: (chemisch -)

Die Matrix ist die Gesamtheit der Bestandteile eines Materials und ihrer chemischen und physikalischen Eigenschaften und deren gegenseitigen Beeinflussungen.

Median

Mengenlehre:

Grundbegriffe der Mengenlehre siehe hier!

Merkmal (characteristic):

Eigenschaft zum Erkennen oder zum Unterscheiden von Einheiten (Charge, Los, Untersuchung einer Grundgesamtheit).
Quantitativ:

• Kontinuierliches oder stetiges Merkmal. D. b., es können alle Merkmalswerte, z. B. in einem Intervall, angenommen werden.
• Diskretes Merkmal; diesem Merkmalstyp werden abzählbare Merkmalsausprägungen zugewiesen.
• Quasi-stetige Merkmale; diskrete Ausprägung, die aber aufgrund ihrer feinen Abstufung wie stetige Merkmale behandelt werden können.

Qualitativ: Attributives oder beschreibendes Merkmal

Gruppierte oder klassierte Merkmale sind zusammengefasste Merkmalsausprägungen. Werden stetige Merkmale gruppiert, können sie als diskret angesehen werden.

Ob ein Merkmal stetig oder diskret ist, kann vom Modell und der Messmethode abhängen. Bei der Wahl der Messmethode, spielt die angemessene Beschreibung der Realität (Modell) und die mathematisch statistische Berechenbarkeit eine Rolle.

Merkmalswert: (characteristic value, auch Prüfergebnis, siehe auch Qualität, Wertdefinitionen und Skalen)

Der Erscheinungsform des Merkmals zugeordneter Wert.

Wertebereich eines Merkmals:

Menge aller Merkmalswerte, die das betrachtete Merkmal annehmen kann.

Für (Untersuchungs-) Merkmale werde oft große lateinische Buchstaben wie z. B. X und für die Ausprägung, also den Wert des Merkmals, kleine lateinische Buchstaben wie in diesem Beispiel x verwendet:

X = Alter des Befragten
x = 45 Jahre

Die Ausprägung x ist die Realisierung des Merkmals X.

Messprobe: (auch Analysenprobe)

Eine Messprobe ist diejenige Probe, deren Gehalt an einem zu bestimmenden Stoff unmittelbar gemessen werden kann. Sie wird aus der Laboratoriumsprobe durch Zusätze von Reagenzien, oder allgem. durch Bearbeitung, erhalten.

Meta-Analyse:

Randomisierte Studien sind die bestmöglichen Voraussetzungen zur Beurteilung eines Therapieerfolges. Systematische Zusammenfassungen dieser randomisierten Studien sind ein wesentlicher Schritt im Erkenntnisgewinn und derartige Zusammenfassungen werden als Übersichtsarbeit oder Review bezeichnet. Übersichtsarbeiten sind dadurch gekennzeichnet, dass in systematischer Weise nach Studien zu einer bestimmten Fragestellung gesucht wird. Diese Studien sollen unabhängig von ihrem Ergebnis in die Bewertung (der Übersichtsarbeit) einfließen. (Diese Forderung ist schwierig einzuhalten, da Studien, die einen negativen Therapieerfolg als Ergebnis zeigen, wenig Chancen auf Veröffentlichung haben!)
Es wir von einer Meta-Analyse gesprochen, wenn die Ergebnisse der einzelnen Studien zu einem gemeinsamen Effekt mit statistischen Methoden zusammengefasst werden.

Methode, 8D-:

Die 8D-Methode beschreibt einen teamorientierten Problemlösungsprozess und legt eine Schrittfolge fest, die durchlaufen werden soll, wenn ein Problem mit unbekannter Ursache offensichtlich wird. Mehr hier....!

Mittelwert (mean), arithmetischen ...

Mittel, geometrisch:

Das geometrische Mittel wird berechnet, wenn die Merkmalswerte x relative Änderungen (Wachstum, Produktionssteigerungen, usw.) oder Zeiten, wie Wartezeiten, sind.
Die Verhältniszahl (relative Änderung) soll als Veränderung im jeweils gleichen zeitlichen Abstand gegeben sein.
Die Berechnung erfolgt nach: 

Mittel, gewogen:

Der gewogene arithmetische Mittelwert wird im Bereich der Datenzusammenfassung dargestellt.

Mittel, harmonisch:

Das harmonische Mittel wird als Mittel für z. B. verschiedene Geschwindigkeiten auf unterschiedlichen Teilstrecken angegeben.
Die Berechnung erfolgt nach:

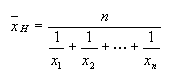Über das harmonische Mittel lässt sich dann die mittlere Geschwindigkeit eines Fahrzeugs ausdrücken, das von A nach B fährt und für verschiedene Streckenabschnitte bestimmte Zeiten benötigt. Folgendes Beispiel zeigt die Berechnung des harmonischen Mittelwertes:

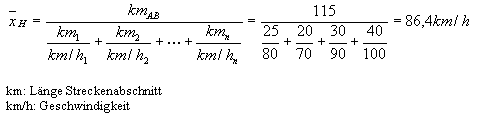Die Durchschnittsgeschwindigkeit für die Strecke von Punkt A nach Punkt B beträgt 86,4 km/h.

Mittelwert, Schwerpunkteigenschaft:

Für den arithmetischen Mittelwert gilt:

D. h., die Summe der Abweichung zwischen x_i und ist Null. Diese Eigenschaft der Einzelwerte (Beobachtungen) wird als Schwerpunkteigenschaft interpretiert. Siehe auch hierzu Standardabweichung. Die Idee, die zur Standardabweichung führt, ist nun, die Summe der Abweichungen der Merkmalswerte vom Mittelwert als Streuungsmaß zu verwenden. Aufgrund der Schwerpunkteigenschaft (es müssen negative wie positive Differenzen vorliegen), wird die Differenz quadriert und somit erhalten alle Abweichungen ein positives Vorzeichen und können summiert werden. Je größer diese Summe ist, desto größer ist die Varianz.
Durch die Quadrierung der Abweichung von reagiert die Standardabweichung (Varianz) allerdings empfindlich auf Extremwerte.

Mittelwert-t-Test:

Mit diesem Test wird die Frage beantwortet, ob 2 Mittelwerte aus Datenreihen vom Umfang n₁ und n₂ unterschiedlich sind. D. h., entstammen beide Mittelwerte einer Grundgesamtheit oder nicht? Mehr dazu hier...!

Mittlere absolute Abweichung (MAD, Mean absolute Deviation):

Als Gütemerkmal einer Prognose kann die mittlere quadratische Abweichung MSE als Kostenfunktion C

über

geschätzt werden. Bei der Beurteil des MAD’s ist die Verteilung, die Auswirkung von Extremwerten (auch wenn sie geringer ist als für den MSE-Schätzer) und eine mögliche Autokorrelation der in das Modell einfließenden Merkmale zu betrachten.

Mittlere quadratische Abweichung (MSE, Mean Squared Error):

Als Gütemerkmal einer Prognose kann die mittlere quadratische Abweichung MSE als Kostenfunktion C

über

geschätzt werden. Bei der Beurteil des MSE’s ist die Verteilung, die Auswirkung von Extremwerten und eine mögliche Autokorrelation der in das Modell einfließenden Merkmale zu betrachten.

Modus:

Der Modus x_mod ist ein Lagemaß und zeigt die Ausprägung (Merkmalswert, Klasse) mit der größten Häufigkeit. Er ist eindeutig, wenn die Häufigkeitsverteilung ein eindeutiges Maximum besitzt. In einem Histogramm (Stab- oder Säulendiagramm) ist er die höchste Säule, die Klasse mit der höchsten Häufigkeit. Besitzt die Ausprägung mindestens ordinales Skalenniveau, kann die Häufigkeitsverteilung auch mehrere voneinander getrennte Maxima besitzen.

Moment siehe Potenzmomente

Multidimensionale Skalierung  siehe hier oder Multivariate Analysenmethoden

Multiple lineare Regression siehe hier...!

Multivariate Daten:

n-dimensionale Daten, d. h. Daten, die aus Beobachtungen von n Merkmale bestehen (siehe auch univariate Daten).

Eine Übersicht über Multivariate Analysemethoden wird hier gegeben.

Nachweisgrenze : (auch Bestimmungsgrenze)

Die Nachweisgrenze stellt den unteren Bereich des Arbeitsbereiches einer Prüfmethode dar (siehe auch Blindwert).
Im einfachsten Fall wird von der Regel ausgegangen, dass der Merkmalswert folgende Eigenschaft hat:

x_i >= 3 s_x

Wenn das Prüfergebnis (Merkmalswert, x_i) wie im obigen Beispiel, 3 mal größer ist als die Standardabweichung s_x, gilt das Ergebnis als gesichert nachgewiesen.
Liegt eine Kalibrierfunktion vor, wird anstatt s_x die Standardwabweichung des Achsenabschnitts s_a eingesetzt.

Neuronale Netze siehe Multivariate Analysenmethoden

Normalverteilung:

Eine wichtige Verteilung in der Statistik ist die Normalverteilung. Und oft geht es um die Frage, ob die beobachteten Werte (z. B. Messwerte) einer Normalverteilung folgen oder nicht. Die Normalverteilung ist eine Dichtekurve, die symmetrisch, unimodal und glockenförmig ist. Diese Art von Dichtkurven, werden durch folgende Dichtfunktion beschrieben:

Form und Lage der Dichtekurve wird durch den Mittelwert und der Standardabweichung festgelegt . Der Mittelwert liegt im Zentrum der Verteilung (= Maximum der Verteilung) und die Dichtekurve ist um so schlanker, je kleiner die Standardabweichung ist.

Folgende Grafik zeigt die Normalverteilung in Abhängigkeit von der Standardabweichung s:

Da in obiger Dichtefunktion Mittelwert und Standardabweichung beliebige Werte annehmen können, existieren beliebig viele unterschiedliche Normalverteilungen. Obige Abbildung ist eine Beispiel für konstantem Mittelwert und 3 verschiedene Standardabweichungen.
Um Verteilungen besser vergleichen zu können, wird die Normalverteilung standardisiert um zur Standardnormalverteilung zu gelangen:

Über diese Standardisierung lassen sich dann die wichtigen Quantile berechnen.

Siehe auch Verteilungen!

Normalverteilung siehe Student-Verteilung

Normalverteilung, Abweichung von

Abweichungen von der Normalverteilung lassen sich, neben der unter obigen Link beschriebenen Methoden, sehr schnell visuell abschätzen. Das kann mittels Histogramm oder über einen Quantil-Quantil-Plot (QQ-Plot) geschehen:

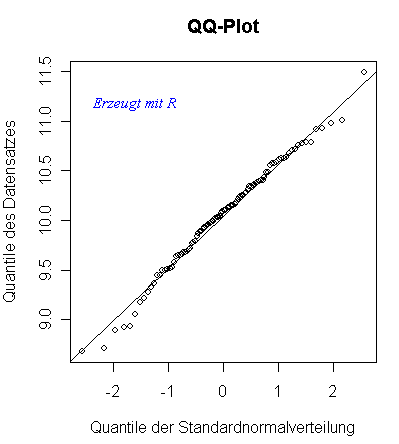Liegen wie im obigen Beispiel-Plot die Beobachtungen (z. B. Messwerte) auf oder ziemlich nahe an der Hilfslinie, kann von einer sehr guten Näherung an die Normalverteilung ausgegangen werden.

Normen:

EN ISO 9000:2000 ff  (Systemnorm)

Normierung, siehe Z-Normierung

Odds Ratio siehe hier!

Ordinalzahl ist eine Menge, die den Ordnungstyp einer wohlgeordneten Menge repräsentiert (Ordnungszahl, siehe auch Skalen).

Ordinate: Bezeichnung für die “vertikale” Koordinate des kartesischen Koordinatensystems (y-Achse).

Ordnungszeichen (Zahlen-), siehe hier!

Panelerhebung:

Eine Panelerhebung ist eine Mehrfacherhebung, die sich auf eine repräsentative Teilauswahl (Panel) bezieht. Die Datenerhebung wird immer zum selben Untersuchungsgegenstand gemacht. Das heißt, es wird eine Mehrfacherhebung zu den selben Merkmalen zu verschiedenen Zeitpunkten mit der gleichen Teilauswahl (d. h. die selben Teilnehmer) durchgeführt.

Der Zweck der Panelerhebung ist, durch die periodische Erhebungen zeitliche Veränderungen sichtbar zu machen. Diese Methode stellt eine Zeitreihenuntersuchung auf Individualebene dar. Dadurch werden Längsschnittdaten erhalten, die als Grundlage für Prognosen zur Marktbeurteilung herangezogen werden können (Handel- / Verbraucherpanels).
Bei Panelerhebungen kommt den Teilnehmern eine besondere Bedeutung zu. Die Bedeutung fängt mit der Gewinnung der Teilnehmer, deren Ersatz bei Teilnehmerausfall und Ende noch nicht mit der Aufrechterhaltung der Teilnahmemotivation. Über einen langen Erhebungszeitraum kann es zu systematischen Verzerrungen kommen, welche dann besonders deutlich werden, wenn ausgefallene Teilnehmer durch neue ersetzt werden. Hier wird auch von Panelmortalität gesprochen. Auch kann es passieren, dass die Teilnehmer ihre Einstellung zum Untersuchungsobjekt ändern (Paneleffekte!)

Pareto-Anaylse:

Die Pareto-Analyse, dargestellt als Pareto-Diagramm, trennt das wenige Wichtige von dem vernachlässigbar Vielem. Synonym wird die Pareto-Analyse auch als ABC-Analyse bezeichnet, weil Einflussgrößen in Gruppen klassiert und in diesen kumuliert werden. Die wichtigsten Gruppen (A, B, C) repräsentieren oft einen beträchtlichen Anteil des Einflusses. Die folgende Abbildung  zeigt ein beispielhaftes Pareto-Diagramm als Ergebnis einer Pareto-Analyse.

Um über eine Pareto-Analyse ein Pareto-Diagramm zu erhalten, müssen Sie

• dass zu untersuchende Problem (Merkmal) festlegen,
• die nötigen Daten erfassen,
• die nötigen Kategorien festlegen, die Daten kategorisieren und kumulieren,
• die Kategorien nach Häufigkeit in absteigender Reihenfolge, wie in Abb.  gezeigt, graphisch darstellen.

Benötigen Sie eine Kategorie „Sonstiges“ als Sammelkategorie, steht sie in der Grafik unabhängig von ihrer Größe, ganz rechts im Diagramm. Verlieren Sie aber nicht die Größe dieser Kategorie aus den Augen! Ab einem gewissen Anteil sollten Sie über eine weitere Aufschlüsselung nach denken.
Das Pareto-Prinzip steht für die 80/20-Regel. Diese besagt, das etwa 80 % der Beeinflussung (der Probleme) durch nur 20 % der beteiligten Faktoren hervorgerufen wird.

Poisson-Verteilung

Population: siehe Grundgesamtheit

Potenzmomente:

Potenzmomente beschreiben die Abweichung von der Normalverteilung.

Präzision (precision):

Ist die Bezeichnung für das Ausmaß der gegenseitigen Annäherung voneinander unabhängiger Merkmalsergebnisse bei mehrfacher Anwendung einer festgelegten Prüfmethode.

Die Präzision beschreibt den zufälligen Fehler (zufällige Abweichung, Varianz).

Es wird unterschieden zwischen Wiederholpräzision und der Vergleichspräzision.

Primär- und Sekundärstatistik:

Wurden die Daten für eine Untersuchung auf Basis von Erhebungen gesammelt, wird von Primärstatistiken (Field Research) gesprochen. Dabei werden folgende Beobachtungsarten unterschieden:

• Beobachtung
  Das zu untersuchende Objekt wird nicht oder nur unwesentlich durch diese Art der Datensammlung beeinflusst. Es verbleibt sozusagen in seiner Umgebung. Eine unwesentliche Einflussnahme stellt das Nehmen einer Stichprobe dar.
   
• Experiment
  Bei einem Experiment nimmt das zu untersuchende Objekt teil. Z. B. in der Medizin, wenn die Wirksamkeit eines neuen Medikamentes erprobt wird. Bei der Planung eines Experimentes können diverse Faktoren, in der Medizin z. B. das Alter des Probanden, berücksichtigt werden. Dadurch besteht ein gewisses Maß an Kontrolle.
   
• Befragung
  Bei dieser Beobachtungsart, wird das Objekt, in diesem Falle Sie und ich, mit sorgfältig formulierten Fragen befragt. Die Fragen müssen so formuliert werden, dass keine oder geringe Verzerrung (Bias) auftreten kann. Die Fragenformulierung gestaltet sich dementsprechend aufwändig.

Von Sekundärstatistiken wird gesprochen, wenn diese Daten nicht zum Zwecke einer statistischen Untersuchung erhoben wurden, sondern z. B. in der behördlichen Verwaltung oder durch eine wirtschaftliche Tätigkeit angefallen sind. Vertraute Beispiele dürften die Kfz-Zulassungszahlen bezogen auf die Automarken oder im Rahmen einer wirtschaftlichen Tätigkeit, die Rohölpreisentwicklung. Die Daten zur Untersuchung sind also schon vorhanden.

Primzahl:

Eine Primzahl p ist eine natürliche Zahl (p > 1), die nur durch sich selbst und durch Eins ohne Rest teilbar ist. Z. B.

p = 2,3,5,7,11,13,17,19,...

Probenahme, Begriffe zur :

Grafische Darstellung der Begriffe zur Probenahme

Los (lot): Menge eines Produkts, das unter Bedingungen entstanden ist, die als einheitlich angesehen werden können. Bei dem Produkt kann es sich beispielsweise um Rohmaterial, um Halbzeug, oder um ein Endprodukt handeln. Unter welchen Umständen die Bedingungen als einheitlich angesehen werden können, lässt sich nicht allgemein angeben. Es kann ein Wechsel des eingesetzten Materials, des Werkzeugs oder eine Unterbrechung des Herstellvorgangs zu anderen Bedingungen führen. Für den Begriff Los wird in bestimmten Branchen auch synonym  “ Charge” oder “Partie” verwendet.

Losumfang (lot size): Anzahl der Einheiten im Los (z. B. 10000 Schrauben oder 5000kg einer chemischen Substanz).

Prüflos (inspection lot): Los, das als zu beutreilende Gesamtheit einer Qualitätsprüfung unterzogen wird.

Probe, Stichprobe (sample):  Eine oder mehrere Einheiten, die aus der Grundgesamtheit (z. B. einer Charge oder Lieferung) oder aus Teilgesamtheiten entnommen werden.

Stichprobenumfang (sample size): Anzahl der Einheiten in der Stichprobe.

Einzelprobe (increment): Durch einmalige Entnahme aus einem Massengut entnommene Probe.

Sammelprobe (bulk sample, gross sample): Probe, die durch Zusammenfassung von Einzelproben oder Teilproben ensteht.

Teilprobe (divided sample): Probe, die durch ein Probeteilungsverfahren aus Einzel- oder Sammelproben gewonnen wird.

Laboratoriumsprobe (laboratory sample): Probe, die als Ausgangsmaterial für die Untersuchung im Laboratorium dient (siehe Messprobe).

Probennahme, Stichprobennahme (sampling): Entnahme einer Probe nach festgelegten Verfahren.

Produktmenge, kartesische -

Proximität:

Proximität ist ein Begriff aus der Distanzanalyse (z. B. Multidimensionale Skalierung, Clusteranalyse) und beschreibt Ähnlichkeits- bzw. Unähnlichkeitskoeffizienten.

Prozessfähigkeit:

Was ist ein fähiger Prozess und wie wird dieser beschrieben? Siehe hier...!

Prüfmethode, -verfahren, -anweisung (inspection instruction):

Beschreibt die Durchführung zur Ermittlung der Merkmalswerte für Prüfmerkmale. Liegt eine Prüfspezifikation vor, ist sie die Grundlage für die Prüfmethode.

Prüfspezifikation (inspection specification):

Festlegung der Prüfmerkmale für die Qualitätsprüfung und gegebenenfalls der vorgegebenen Merkmalswerte sowie erforderlichenfalls der Prüfverfahren (-methode).

p-value (p-Wert):

Hypothesenentscheidung auf Basis des p-values in der Anwendung von Statistikprogrammen wie z. B. R siehe hier...!

QQ-Plot siehe hier!

Qualität (quality):

Ist die Gesamheit der Merkmale und Merkmalswerte, bzw. deren Ausprägung, eines Objektes (z. B. Produkt, Dienstleistung) bezüglich seiner Eignung, festgelegte und vorausgesetzte Erfordernisse zu erfüllen (nach DIN 58936 Teil 1)

Qualitätsmerkmal (quality characteristic):

Ist ein Merkmal, das die Qualität eines Objektes beschreibt. Es ist damit ein Element der Gesamtheit aller die Qualität eines Objektes charakterisierender Kennzeichen und Eigenschaften (nach DIN 58936 Teil 1).

Qualitätsprüf-Zertifikat:

Bescheinigung über das Ergebnis einer Qualitätsprüfung, das gegenüber dem Abnehmer oder Auftraggeber als Nachweis über die Qualität eines Produkts dient. Ein Zertifikat enthält Angaben über:

• Aussteller des Qualitätsprüf-Zertifikats/Datum
• Hersteller/Auftragnehmer (Lieferer)
• Abnehmer/Auftraggeber/Besteller/Betreiber
• Auftrags-/Bestell-Nummer
• Liefergegenstand, Stückzahl usw.
• Qualitätsforderungen
• Prüfspezifikationen
• Art des Qualitätsprüf-Zertifikats, z. B. “Herstellerzertifikat M nach DIN 55 350 Teil 18”
• gegebenenfalls spezielle Qualitätsmerkmale
• Prüfergebnisse

Qualitätssicherung (quality assurance):

Ist die Gesamtheit der Tätigkeiten des Qualitätsmanagements, der Qualitätsplanung, der Qualitätslenkung und der Qualitätsprüfung. Qualitätssicherung ist als integrierter Prozess in der Wertschöpfungskette zu verstehen.

Qualitätsmanagement ist der Aspekt des Gesamtmanagements, der die Qualitätspolitik festlegt und zur Ausführung bringt (siehe QM-System).

Qualitätsplanung bedeutet auswählen, klassifizieren und gewichten der Qualitätsmerkmale und konkretisieren der Qualitätsanforderung unter Berücksichtigung von Anspruch und Realisierungsmöglichkeiten.

Qualitätslenkung bedeutet, Überwachung der Qualitätsmerkmale im Hinblick auf die gegebenen Forderungen sowie gegebenenfalls Korrekturmaßnahmen.

Qualitätsprüfung bedeutet festzustellen, inwieweit das Objekt die Qualitätsforderung erfüllt.

(Nach DIN 55350 Teil 11 und DIN 58936 Teil 1)

Qualitätssicherungssystem (quality control system):

Ein Qualitätssicherungssystem beschreibt die festgelegte Organisation zur Durchführung der Qualitätssicherung.

Quantile, Quartile:

Ein Quantil (Unterteilung der Grundgesamtheit) oder Quartil (Quartile teilen die Grundgesamtheit in 4 gleich große Teile) ist ein Lokalisationsmaß einer stetigen Verteilung, bei dem die Wahrscheinlichkeit p für einen Wert <= p oder => 1-p ist.

Der Median ist das 50%-Quantil, d. h., hier sind 50% der Werte <= dem Median und 50% der Werte => dem Median.
Der Quartilabstand ist gegeben durch den Abstand zwischen dem oberen und unterem Quartil:

x_0,75 - x_0.25 = Quartilabstand

Der Quartilabstand gibt an, wie die mittleren 50% der Beobachtungen streuen (siehe auch Boxplot).
Im Zusammenhang mit dem Median werden, wenn die Anzahl n der Werte >= 20 ist (Empfehlung), oft die Quantile Q₁, Q₂ = Median und Q₃ angegeben:

Ist die Verteilung annähernd symmetrisch zum Median, sind Q₁ und Q₃ gleich weit vom Median entfernt. Siehe auch QQ-Plot!

Quantoren:

Quantoren ist ein Begriff aus der Logik und ermöglichen das kurze Formulieren von Existenz- und Allaussagen:

Beispiel:

Es gibt eine Zahl, die Teiler von 12 ist:

Siehe auch Junktoren, Wahrheitswerttabelle  und Relationen.

Radiant rad, Beziehung Radiant (Bogemaß) und Grad.

Rangkorrelationskoeffizient, siehe hier!

Ratingverfahren (Likert-Skala (nach Renisis Likert)):

Verfahen zur Erhebung von Ähnlichkeitsurteilen, siehe MDS (Multidimensionale Skalierung).

Rechnen mit fehlerbehafteten Zahlen, Fehlerfortpflanzung:

Um den Fehlerbereich für fehlerbehaftete Zahlen bei Anwendung der vier Grundrechenarten auftritt abzuschätzen, werden zwei parallele Rechnungen durchgeführt. Eine mit der unteren Fehlerschranke und eine mit der oberen Fehlerschranke. An folgenden Beispieldaten, wird die Auswirkung der Fehlerfortplanung gezeigt:

50 +- 3         (Wertebereich von 47 bis 53)
40 +- 2         (Wertebereich von 38 bis 42)

Addition:

Die Summe beider Zahlen liegt zwischen

• 47 + 38 = 85
  und
• 53 + 42 = 95.

Der relative Fehler der Summe beträgt

(95 - 85) / (95 + 85) = 10 / 180 = 0,0556 = 5,56 %.

Subtraktion:

Die Differenz wird überkreuz ermittelt:

• 47 - 42 = 5
• 53 - 38 = 15

Der relative Fehler der Differenz beträgt

(15 - 5) / (15 + 5) = 10 / 20 = 0,5 = 50 %.

Multiplikation:

Das Produkt liegt in den Grenzen von

• 47 * 38 = 1786
  und
• 53 * 42 = 2226.

Der relative Fehler des Produktes liegt bei

(1786 - 50 * 40) / 50 * 40 = (1786 - 2000) /2000 = -0,107 = - 11,7 %
und
(2226 - 50 * 40) / 50 * 40 = (2226 - 2000) / 2000 =  0,113 = 11,3 %.

Division:

Die Quotienten betragen (überkreuz)

• 47 / 42 = 1,1191
  und
• 53 / 38 = 1,3947.

Der relatve Fehler beträgt dann

(1,1191 - 50 / 40) / (50 / 40) = (1,1191 - 1,25) / 1,25 = -0,105 = -10,5 %
und
(1,3947 - 50 / 40) / (50 / 40) = (1,3947 - 1,25) / 1,25 = 0,116 = 11,6 %.

Aus diesen Beispielen ist leicht ersichtlich, dass das Rechnen mit fehlerbehafteten Zahlen bezüglich der Subtraktion besonders kritisch zu betrachten ist.

Referenzmaterial (reference material):

Ein Referenzmaterial ist eine Substanz, deren Eigenschaft / Eigenschaften so genau festgelegt oder bekannt sind, dass sie zur Kalibrierung von Messgeräten und Kontrolle der Prüfmethode verwendet werden kann.

Regelkarte:

Qualitätsregelkarten sind Werkzeuge zur statistischen Prozesskontrolle, mehr dazu hier...!

Regression, logistische siehe Multivariate Analysenmethoden

Regressionsanalyse siehe Korrelations- und Regressionsanalyse oder Multivariate Analysenmethoden

Regressionsbaum siehe hier!

Relationen:

Durch Relationen (relationale Operatoren) werden Beziehungen zwischen Zahlen dargestellt:

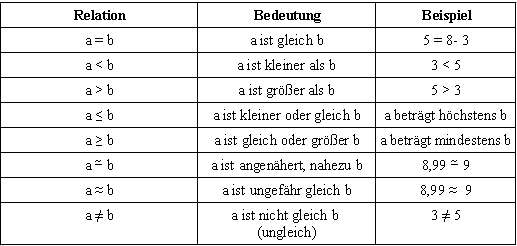Relatives Risiko siehe hier!

Reliabilität:

Reliabilität bedeutet, dass die Beobachtungen (Daten) zuverlässig ermittelt werden. Zuverlässig bedeutet, die Daten mit einer möglichst hohen Güte und Genauigkeit zu bestimmen.  D. h, es müssen Bedingungen vorliegen oder geschaffen werden, die Beobachtungsdaten mit einem möglichst kleinen Fehler bestimmt werden können.

Validität und Reliabilität stehen in einer engen Beziehung. Wird eines von beiden vernachlässigt, können die gesamten Beobachtungen wertlos sein.

Residuen:

Als Residuen e wird die Abweichnung zwischen der Zielgröße y (Vorgabe einer Kalibrierung) und dem berechneten Wert der Zeilgröße y^o = a + bx, bezeichnet:

e_i = y_i - y^o_i

Mit ihrer Hilfe können Aussagen über die Korrektheit des linearen Modells gemacht werden (siehe Korrelation). Ist das Modell korrekt, müssen sich die Werte von e_i im gesamten Bereich von y^o_i ohne erkennbare Struktur um 0 sammeln.

Richtiger Wert (conventional true value):

Wert für Vergleichszwecke, dessen Abweichung vom wahren Wert für den Vergleichszweck als vernachlässigbar betrachtet wird.

Richtigkeit (trueness, accuracy of the mean):

Die Richtigkeit ist eine Bezeichnung für das Ausmaß der Annäherung des Mittelwertes der Merkmalergebnisse an den Bezugswert, wobei dieser je nach Festlegung oder Vereinbarung der richtige oder ein festgelegter Wert sein kann.

Die Richtigkeit beschreibt den systematischen Fehler (systematische Abweichung).

RPZ, Risikoprioritätszahl:

Maßzahl einer FMEA, Fehlermöglichkeits- und Einflussanlayse (Failure Mode and Effects Analysis), mehr dazu hier!

Schätzen:

• Punktschätzung:
  Eine Punktschätzung ist das Schätzen eines Wertes für einen unbekannten Parameter auf Basis der vorliegenden Verteilung über eine Stichprobe. Der Schätzwert ist ist das Ergebnis (die Realisierung) dieser Punktschätzung des unbekannten Parameters. Es ist unbekannt, wie gut der Schätzwert dem wahren Parameter nahe kommt. Siehe hierzu auch das Gesetz der Großen Zahlen. Zur Abschätzung der Abweichung vom wahren Wert, wird die Punktschätzung durch die Intervallschätzung ergänzt.
  Einfache Beispiele der Punktschätzung ist die Berechnung des Mittelwertes (Schätzfunktion) und der Standardabweichung.
   
• Intervallschätzung:
  In dem durch die Intervallschätzung geschätztem Intervall, soll der Parameter der Punktschätzung (der Schätzwert) mit einer bestimmten Vertrauenswahrscheinlichkeit enthalten sein. Dieses Intervall heißt Konfidenzintervall oder Vertrauensbereich. Ein Beispiel ist die Schätzung des Vertrauensbereich um den Mittelwert.
   

Gewünschte Eigenschaften einer Schätzfunktion:

• Erwartungstreue -> möglichst geringer systematischer Fehler
• Effizienz -> möglichst geringe Varianz, auch bei kleinem Stichprobenumfang
• Konsistent -> mit wachsendem Stichprobenumfang dem wahren unbekannten Parameter entgegen streben (konvergieren)
• Suffizienz, Robust -> alle Informationen der Stichprobe nutzen und robust gegenüber Abweichungen (vom angenommenen Modell)

Schiefe:

Siehe Abweichung von der Normalverteilung.

Schlussregeln (mathematische -):

Eine Schlussregel ist eine Aussagelogik wie “Wenn a eine hinreichende Bedingung für b ist und a wahr ist, dann ist auch b wahr!”

Schwerpunkteigenschaft des Mittelwerts

Shapiro-Wilk-Test:

Mit dem Shapiro-Wilk-Test wird die Hypothese geprüft, ob die Beobachtungen X normalverteilt sind. Dazu wird die Verteilung des Quotienten aus zwei Schätzungen der Varianz s² betrachtet: das Quadrat einer kleinsten Fehlerquadratschätzung für die Steigung der Regressionsgraden im QQ-Plot und die Stichprobenvarianz. Liegt Normalverteilung vor, sollten beide Schätzung nahe zusammenliegen und der Quotient W sollte 1 oder nahe bei 1 liegen.

Der Quotient W liegt nahe bei 1 und der p-Wert (p-value) als Wahrscheinlichkeitsaussage zum Zutreffen der Hypothese ist genügend groß. Weicht W deutlich von 1 ab und geht der p-Wert deutlich in Richtung 0 (z. B. < 0,05) ist von einer Abweichung von der Normalverteilung auszugehen.

Signifikanzniveau: siehe Wahrscheinlichkeit

Six Sigma, ein methodisches Vorgehen zur Prozessverbesserung, siehe hier...!

Skalen:

Spannweite (range) R:

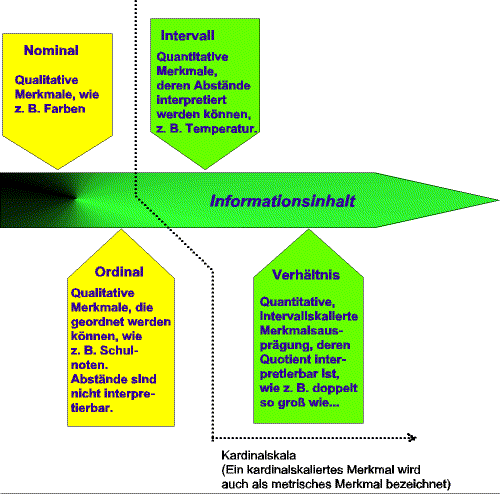Ist die Differenz aus dem größten und dem kleinsten Merkmalswert: R = x_max - x_min

Spearman, Rangkorrelationskoeffizient nach ...

Splines, Regressionanalyse über die flexible Modellierung mit ...

Standardabweichung: siehe Statistik-Basis

Statistik, Die drei Bereiche der -:

Einen kleinen Überblick über die drei Statistikbereiche soll folgende Grafik geben:

Statistische Prozessüberwachung (statistical process control, SPC):

Sie ist der Teil der Qualitätskontrolle / -lenkung, bei der statistische Verfahren zur Planung und Aus-/Bewertung eingesetzt werden (nach DIN 58936 Teil1, siehe auch Prozessfähigkeit und Regelkarten!).
Natürlich ist die statistische Prozesskontrolle, wie häufig angenommen, nicht nur ein Qualitätsmanagementwerkzeug für den Produktionsbereich, sondern kann und sollte auf alle Geschäftsprozesse angewendet werden. Folgende Präsentation kann zur Motivation dienen: Statistical Quality Control SPC (OpenOffice - animiert) / Statistical Quality Control SPC (PDF)

Sterbetafel:

Zur Sterbetafel im Rahmen der Weibullverteilung geht es hier....!

Stetigkeit

Stichprobe: siehe Probennahme

Stichprobenraum: siehe Ergebnisraum

Strukturgleichungsmodelle siehe Multivariate Analysenmethoden

Stochastik: Teilgebiet der Mathematik, das sich mit zufälligen Ereignissen befasst (Wahrscheinlichkeitsrechnung).

Student-Verteilung, t-Verteilung (Tabelle der t-Verteilung)

Summenformel, Arithmetische -

Summenformel, Geometrische -

Summenhäufigkeit, kumulierte Häufigkeit:

Über ein Histogramm können Sie einen visuellen Eindruck über die Verteilung Ihrer Beobachtungen gewinnen (siehe auch Skalen). Möchten Sie hingegen wissen, wie viele Beobachtungen unterhalb oder einschließlich einer bestimmten Grenze (Klasse) liegen, hilft die kumulierte Häufigkeit weiter. Zur Bildung der kumulierten Häufigkeiten werden die Beobachtungen beginnend mit der kleinsten Ausprägung in aufsteigender Reihenfolge aufaddiert (kumuliert).

Die folgende Tabelle zeigt ein Beispiel:

Die kumulierte Summe für n = 4 setzte sich zusammen aus der Summe = n1+n2+n3+n4 = 2+5+6+11 = 24. D. h., bis einschließlich n₄ liegen 24 Beobachtungen vor!

Formaler lässt sich das als Summenhäufigkeits-Funktion ausdrücken:

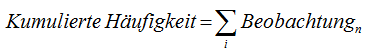Systematische Abweichung (systematic deviation, systematic error):

Siehe Richtigkeit.

Systematische Abweichungen weisen bei definierter Vorgehensweise (z. B. gleiche Prüf- methode) gleiches Ausmaß und Vorzeichen auf. Bei quantitativen Merkmalswerten ist die systematische Abweichung, unter Berücksichtigung der vorangemachten Ausage, gleich der Differenz aus Erwartungswert und richtigem bzw. wahrem Wert.

Teilerfremd:

Zwei natürliche Zahlen sind teilerfremd, wenn es keine natürliche Zahl außer der 1 gibt, die beide Zahlen teilt. Ein Bruch zweier teilerfremder Zahlen kann nicht weiter gekürzt werden.

Test:

• Parametrischer Test:
  Bei dieser Gruppe von Tests ist das Vorliegen und Bekanntsein einer bestimmten Verteilung Voraussetzung. Als Beispiele seien hier der t-Test, der Shapiro-Wilk-Test oder auch die Ausführungen unter Schätzen genannt. Die Ausprägung der Beobachtung muss kardinalskaliert sein.
   
• Nichtparametrischer Test:
  Bei diesen Tests wird keine Annahme über die genaue Form der Verteilung gemacht. Deswegen werden diese Tests auch verteilungsunabhängige oder verteilungsfreie Tests genannt. Diese Tests sind an weniger Voraussetzungen - z. B. der Normalverteilung - gebunden. Damit sind die Aussagen nur unter bestimmten Voraussetzungen gültig und müssen für jeden Test entsprechend belegt werden. Die Ausprägung der Beobachtung ist von einem niedrigen Skalenniveau als kardinalskaliert.

Term:

Ein Term ist ein sinnvoller Ausdruck, der Zahlen, Variablen, Symbole (auch mathematische Verknüpfungen) enthalten kann:

f(x) = a + bx

a:   konstanter Term
bx: linearer Term

Umgangssprachlich: Ein Term ist das, was Bedeutung trägt!

Test, Das Prinzip des -

Welchem Prinzip ein statistischer Test folgen sollte, finden Sie hier!

Theorem (= Lehrsatz):

Ein Theorem ist ein allgemeiner Lehrsatz, ein Bestandteil einer wissenschaftlichen Theorie oder Lehrmeinung: “Der erklärende Satz einer Aussage / eines Systems”

Theorem = Lehrsatz = Satz

Ein Satz muss mit den Axiomen der Theorie und mit den Schlussregeln der Theorie bewiesen werden.

Toleranz (tolerance): Höchstwert minus Mindestwert und auch obere Grenzabweichung minus untere Grenzabweichung.

Toleranzbereich (tolerance zone): Bereich zugelassener Werte zwischen Mindestwert und Höchstwert.

Trendtest siehe hier!

t-Test für

... Differenzen siehe hier!

... Sollwerte siehe hier!

... den Korrelationskoeffizient:

Über den t-Test zur Prüfung der Korrelationskoeffizienten kann geprüft werden, ob ein statistisch signifikanter Zusammenhang zwischen den Ausprägungen (Realisierungen) x_i und y_i der Merkmale X und Y besteht. Weiteres finden Sie hier!

Tupel, n-Tupel siehe hier!

t-Verteilung siehe Student-Verteilung

Unabhängige identische Wiederholung:

Näheres finden Sie hier!

Univariate Daten:

Eindimensionale Daten, d. h. Daten, die aus Beobachtungen eines einzelnen Merkmals bestehen (siehe auch multivariate Daten).

Ursache-Wirkungs-Diagramm: (Fischgräten- oder Ishikawa-Diagramm, K.Ishikawa 1915-1989)

Durch ein Ursache-Wirkungs-Diagramm kann die Suche nach Fehlerursachen in einem Prozessablauf erleichtert werden. Es ist möglich, auf Basis dieses Diagramms auch komplexe Zusammenhänge zu visualisieren und dadurch zu analysieren. Dabei wird wie im folgenden Bild gezeigt, von den Ursachen, z. B. den 5 M`s, auf das Ereignis (Problem) geschlossen:

Validität:

Validität bedeutet einfach ausgedrückt, die Daten zu messen (beobachten), die Gegenstand der Untersuchung sind. Wenn der Beobachter an der Körpergröße des Menschen interessiert ist, soll sie von den Füßen bis einschließlich des Kopfes gemessen und nicht der Bauchumfang bestimmt werden.
Ist das direkte Bobachten (Messen) der gewünschten Eigenschaft nicht möglich, kommt möglicherweise eine Hilfsgröße (Proxy-Variable) in Betracht. Das Bruttoinlandsprodukt ist ein Beispiel für eine Proxy-Variable, denn an welcher einzelnen Eigenschaft soll der Wohlstand eines Volkes festgemacht werden?

Validität und Reliabilität stehen in einer engen Beziehung. Wird eines von beiden vernachlässigt, können die gesamten Beobachtungen wertlos sein.

Variable:

Eine Variable (lat.: variabilis) wird als Platzhalter oder als eine Veränderliche in einem mathematischen Ausdruck  verstanden. Im statistischen Zusammenhang, ist eine Variable der Träger der Ausprägung einer Beobachtung. Soll z. B. in einem bestimmten Kontext die Körpergröße der Bevölkerung ermittelt werden, ist die Beobachtung die Körpergröße in cm, die Variable vielleicht Größe und die Ausprägung für eine Beobachtung (aus der Stichprobe) möglicherweise 182. Derartige Variablen sind direkt beobachtbar, d. h., messbar und werden auch manifeste Variablen genannt.

Latente Variablen sind Variablen, die nicht direkt beobachtbar sind, wie z. B. Qualität, Intelligenz, Solidarität, usw.. Sie müssen durch die sogenannte Operationalisierung zunächst messbar gemacht werden. Die in der Operationalisierung gemachten Annahmen werden als Messmodell bezeichnet. Das Messmodell beschreibt zur indirekten Messung der  latenten Variable, wie z. B. dem Intelligenzquotienten, Merkmale, die direkt beobachtet werden können (manifeste Variablen). Diese manifesten Variablen werden auch Indikator-Variablen genannt.  Proxy-Variable ist ein Synonym für die latente Variable.
Das folgende Bild zeigt als Übersicht ein einfaches Messmodell zur Messung der latenten Variable Intelligenz. Die Intelligenz wirkt auf die jeweilige Kompetenz, die wiederum messbar ist:

Ein Video zum Thema latente Variable finden Sie hier!

Varianz: siehe Statistik-Basis

Varianzanalyse siehe Multivariate Analysenmethoden

Variationskoeffizient siehe hier!

Vergleichsbedingungen:

Bei der Gewinnung von unabhängigen Merkmalswerte gelten folgende Bedingungen: festgelegte Prüfmethode, identisches Objekt (Material), verschiedene Prüfer (Beobachter), eventuell verschiedener Prüfausstattung (Geräte) und verschiedene Orte (Labors).

Vergleichspräzision (reproducibility):

Die Vergleichspräzision ist die Bezeichnung für das Ausmaß der gegenseitigen Annäherung der Merkmalswerte unter Vergleichsbedingungen.

Verknüpfungen , logische -, siehe hier!

Verteilungen, Gipfeligkeiten von:

Folgende Grafik zeigt mögliche Häufigkeitsverteilungen und deren Bezeichnungen:

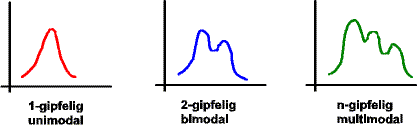Verteilung, - (Chi²-)

Verteilung, Binomial-

Verteilung, geometrische

Verteilung, hypergeometrische

Verteilung, Normal-, Student- (t-)

Verteilung, Poisson-

Verteilung, Weibull-

Vertrauensbereich, Konfidenzbereich (confidence interval):

Unter Vertrauensbereich wird ein aus Stichprobenwerten berechnetes, d. h. in der Lage und Breite zufälliges Intervall, das den wahren aber unbekannten Parameter mit einer vorgegebenen Wahrscheinlichkeit, der Vertrauenswahrscheinlichkeit, überdeckt (einschließt), verstanden. Die Grenzen des Intervalls werden Vertrauensgrenzen (confidence limits) genannt.

Siehe Berechnung Vertrauensbereich für den Mittelwert

Verzerrung siehe Bias

Vorzeichenregel siehe hier!

Wahrer Wert (true value):

Tatsächlicher Merkmalswert; ist in der Regel aber nur ein ideeller Wert, weil er sich praktisch nicht ermitteln lässt. Es können i. d. R. zu dessen Ermittlung nicht alle Faktoren, die zur Ergebnisabweichung beitragen, vermieden werden (nach DIN 55350 Teil12).

Wahrscheinlichkeit:

Die Wahrscheinlichkeitsverteilung einer Zufallsvariablen gibt an, mit welcher Wahrscheinlichkeit die Werte der Zufallsvariablen angenommen werden. Diese Wahrscheinlichkeitsverteilung wird durch die Verteilungsfunktion eindeutig definiert:

F(x) = P(X <= x)

F(x) gibt die Wahrscheinlichkeit an, dass die Zufallsvariable X einen Wert kleiner oder gleich x annimmt. Nimmt die Zufallsvariable x diskrete Werte an, wird von einer Wahrscheinlichkeitsfunktion (probability function, frequency function) gesprochen. Die Verteilungsfunktion wird durch Aufsummieren der Wahrscheinlichkeiten

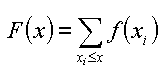ermittelt. Für stetige Zufallsvariablen wird die Verteilungsfunktion durch Integration über die Wahrscheinlichkeitsdichte berechnet:

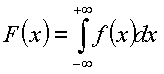Wahrscheinlichkeit: Mit welcher Wahrscheinlichkeit tritt ein Ereignis aus der Anzahl möglichen Ereignisse ein?
Der Wahrscheinlichkeitsbegriff kann in eine objektive und subjektive Wahrscheinlichkeit separiert werden:

• Objektiv: Die Wahrscheinlichkeit mit einem Würfel eine 6 zu werfen, beträgt 1:6.
• Subjektiv: Wahrscheinlich werde ich heute Abend ins Kino gehen!

Im ersten Beispiel ist der objektive Charakter deutlich erkennbar und im zweiten Beispiel, der subjektive durch die “Alltagsaussage /-annahme” ebenfalls.

Wahrscheinlichkeit: Vertrauens- und Irrtumwahrscheinlichkeit

Wahrscheinlichkeiten:

• A-priori-Wahrscheinlichkeit:
  Wird eine Wahrscheinlichkeit P auf logischem Wege ermittelt, wird von einer A-priori-Wahrscheinlichkeit gesprochen (theoretische Wahrscheinlichkeit). Nehmen wir als Beispiel den Wurf einer Münze. Wir gehen von der Voraussetzung aus, dass beide Seiten (Kopf/Wappen und Zahl) gleichwertig sind, d. h., keine Seite wird durch die Prägung bevorzugt! Wird die Münze geworfen, kann das Ereignis, das Ergebnis des Wurfes, mit gleicher Wahrscheinlichkeit P Wappen oder Zahl annehmen. Die Wahrscheinlichkeit dass z. B. das Ereignis = Zahl ist, beträgt

P_(Zahl) = Ereignis / mögliche Ereignisse = 1/2 = 0,5 (50%)

Wir nehmen eine A-priori-Wahrscheinlichkeit P von P = 0,5 an!

• A-posteriori-Wahrscheinlichkeit:
  Bleiben wir bei dem Beispiel. Zeigt die Münze starke Abnutzungserscheinungen, darf die oben beschriebene theoretische Wahrscheinlichkeit, die A-priori-Wahrscheinlichkeit, nicht mehr erwartet werden. D. h., wir gehen nicht mehr davon aus, dass mit einem beliebigen Münzwurf die Wahrscheinlichkeit P für Ereignis = Zahl nicht mehr P_(Zahl) = 0,5 (50%) beträgt!
  Um die Wahrscheinlichkeit P für den Wurf Zahl zu bestimmen, hilft nur noch das Experiment weiter:
  Es wird n-mal (Vielleicht 100-mal?) die Münze geworfen und das Auftreten von Wappen und Zahl gezählt. Tritt idealerweise 50-mal das Ereignis Zahl ein, ist die empirische Wahrscheinlichkeit, oder auch A-posteriori-Wahrscheinlichkeit

P_(Zahl) = Anzahl Ereignis Zahl / Anzahl der Münzwürfe = 50 / 100 = 0,5

Hier sind wir von dem idealen Fall der Gleichverteilung zwischen Wappen und Zahl ausgegangen. In der “realen” Welt, strebt die relative Häufigkeit des Wurfs Zahl gegen die wahre Verteilung zwischen Wappen und Zahl mit steigender Anzahl n der Münzwürfe.

Darauf basierend, lässt sich allgemein folgender Grenzwert für die A-posteriori-Wahrscheinlichkeit definieren:

Wahrheitswerttafel:

Für die (logischen) Aussagen A und B werden die Verknüpfungen gemäß folgender Wahrheitswerttafel mit w = wahr und f = falsch erklärt:

Die Verknüpfung A => B wird als logische Implikation (Folgerung) bezeichnet; es sind folgende Sprechweisen üblich:

• aus A folgt B
• A impliziert B
• wenn A gilt, dann gilt auch B
• A ist eine hinreichende Bedingung für B
• B ist eine notwendige Bedingung für A

Die Verknüpfung A <=> B ist eine abgekürzte Schreibweise für A => B und B => A. Sprechweisen für äquivalente Aussagen sind:

• B gilt genau dann, wenn A gilt
• B gilt nur dann, wenn A gilt
• B ist eine hinreichende und notwendige Bedingung für A

Übersicht über wichtige Junktoren (Bindewörter in der formalen Logik):

Weibull-Verteilung:

Lebensdauerverteilungen lassen sich die Weibullverteilung darstellen, mehr dazu hier...!

Wertdefinitionen:

Istwert (actual value): Ermittlungsergebnis eines quantitativen Merkmals.

Sollwert (desired value): Wert eines quantitativen Merkmals, von dem die Istwerte dieses Merkmals so wenig wie möglich abweichen sollen (siehe Toleranzbereich).

Richtwert (standard value): Wert eines quantitativen Merkmals, dessen Einhaltung durch die Istwerte empfohlen wird, ohne dass Grenzwerte vorgegeben sind.

Grenzwert (limiting value): Mindestwert oder Höchstwert.

Mindestwert (lower limiting value): Kleinster zugelassener Wert eines quantitativen Merkmals.

Höchstwert (upper limiting value): Größter zugelassener Wert eines quantitativen Merkmals.

Wiederholpräzision (repeatability, wirhin-run precision):

Die Wiederholpräzision ist die Bezeichnung für das Ausmaß der gegenseitigen Annäherung der Prüfergebnisse unter Wiederholbedingungen.

Wiederholbedingungen:

Bei der Gewinnung von unabhängigen Prüfergebnissen gelten folgende Bedingungen: festgelegte Prüfmethode, identisches Objekt (Material), der gleiche Prüfer (Beobachter), die gleiche  Prüfausstattung (Geräte) und der gleiche Ort (Labor).

Wiederkehrende Prüfung:

Qualitätsprüfung nach für die Wiederkehr vorgegebenen Regeln in einer Folge von vorgesehenen Qualitätsprüfungen an derselben Einheit (Lot, Charge).

Wiederholungsprüfung:

Qualitätsprüfung nach unerwünschtem Ergebnis der vorausgegangenen in einer Folge von zugelassenen Qualitätsprüfungen an derselben Einheit (Lot, Charge).

Wilcoxon-Test:

Tests für den Vergleich zweier verbundener Stichproben, Vorzeichen-Rang-Test nach Wilcoxon.

Wölbung:

Siehe Abweichung von der Normalverteilung.

Z-Normierung:

Oft besteht die Notwendigkeit Merkmalswerte (Merkmalsausprägungen) zur besseren Beurteilung oder für statistische Verfahren derart zu normieren, dass der Mittelwert den Wert 0 und die Standardabweichung den Wert 1 annimmt. Diese Standardisierung oder Z-Normierung wird über folgende Formel durchgeführt:

Zahlen, hier eine Übersicht über die Einteilung der Zahlen.

Zahlen, Das Gesetz der Großen - :

Das Gesetz der Großen Zahlen wird am Beispiel des arithmetischen Mittels dargestellt:

 = 1/n (X₁ + ... + X_n)

 ist der durchschnittliche Wert von X, des Merkmals, bei n (= Anzahl) Versuchen. Nach der “Versuchsdurchführung” liegt die Realisierung, also der Wert (die Merkmalsausprägung), vor:

Strebt nun n -> , oder wird zumindest sehr groß, strebt der Erwartungswert des Mittelwerts

E(_n) =   und die Varianz   gegen 0.

Einfach ausgedrückt, bedeutet dies, dass mit einer hohen Anzahl von Werten, die Schätzung des Mittelwerts der Merkmalausprägung und und die dazugehörige Standardabweichung immer besser wird. Je mehr Ereignisse, desto näher an den Erwartungswert!

In diesem Beispiel sagt das Gesetz der großen Zahlen aus, dass mit dem Streben von n -> die Wahrscheinlichkeit P für -> gegen 1 strebt (konvergiert):

Zeitreihenanalyse siehe hier!

Zeitreihe, Stationarität

In der Zeitreihenanalyse wird davon ausgegangen, dass die Beobachtungen X_t eines zufälligen Prozesses zu verschiedenen Zeitpunkten t_n voneinander abhängen. Diese Beobachtungen folgen einer bestimmten Verteilung, die im Allgemeinem unbekannt ist. Die Beobachtung X_t stellt eine Ausprägung des Merkmals X zum Zeitpunkt t dar und somit kann nicht auf die Momente Erwartungswert und Varianz geschlossen werden.
Damit dennoch statistische Verfahren bei der Betrachtung von Zeitreihen angewendet werden können, werden Eigenschaften definiert, die durch Zeitreihen erfüllt werden müssen. Diese Eigenschaften beziehen sich auf die Momente Erwartungswert, Varianz und Autokovarianz (bzw. Korrelation). Es muss immer bedacht werden, dass der Erwartungswert, die Varianz / Kovarianz der Zeitreihe für X_t zu jedem Zeitpunkt t verschieden sein kann.

Ein statistischer Prozess Prozess (dem die Zeitreihe zugrunde liegt) wird als schwach stationär bezeichnet, wenn der Mittelwert und die Varianz zeitunabhängig sind und die Kovarianz lediglich vom zeitlichen Abstand (Lag) zwischen den Punkten t und t+1 abhängt, aber nicht vom Zeitpunkt t an dem die Beobachtung X gemacht wird.

Von einem streng stationären Prozess wird gesprochen, wenn zu jedem Zeitpunkt t die gleiche Verteilung vorliegt.

Verlieren Sie bezüglich der Stationarität nicht die Eingangsbemerkung aus den Augen!

Zeitreihe, weißes Rauschen (White noise)

In der Zeitreihenanalyse wird das weiße Rauschen als der einfachste statistische Zeitreihen-Prozess  betrachtet. Das weiße Rauschen besteht aus zeitlich zufälligen, unkorrelierten Beobachtungen mit dem  Erwartungswert  Null und einer konstanten Varianz. Dieser Prozess ist schwach stationär. Die Autokorrelationsfunktion ist immer Null, ausgenommen für Lag = 0.

Für den Prozess „weißes Rauschen“ kann keine Aussage über den zukünftigen Verlauf des Prozesses aus der Vergangenheit gemacht werden, da die Autokorrelationsfunktion keine Struktur aufweist.

Zwischenprüfung:

Qualitätsprüfung während der Realisierung einer Einheit (Lot, Charge).

Zufällige Abweichung (random deviation, random error):

Zufällige Abweichungen weisen bei definierter Vorgehensweise (z. B. gleiche Prüfmethode) ein zufälliges Ausmaß und Vorzeichen auf. Bei quantitativen Merkmalswerten ist die zufällige Abweichung, unter Berücksichtigung der vorangemachten Ausage, gleich der Differenz aus Merkmalswert und richtigem bzw. wahrem Wert.

Zufallsstichproben:

Zufallsstichproben sind Teile einer Grundgesamtheit, die durch einen Auswahlprozess mit Zufallsprinzip aus dieser entnommen und stellvertretend, repräsentativ für die Grundgesamtheit sind (siehe Grundgesamtheit und Beispiel).

Zufallsvariable:

Die Zufallsvariable ist ein Grundbegriff der Statistik mit folgender Bedeutung: Der Wert einer Zufallsvariablen, z. B. ein Merkmalswert, wird bei der Durchführung eines Versuches ermittelt (siehe auch Zufallsvorgang).

Je nach Art des Versuchs (Experiment, Beobachtung) sind die möglichen Werte der Zufallsvariablen ein einzelner Wert einer Größe (beim Messen), einer Zahl (beim Zählen), eine Ausprägung (bei der Bestimmung eines qualitativen Merkmals) usw. oder auch Paare, Tripel, Quadrupel, n-Tupel solcher Werte.

Eine Zufallsvariable, die nur abzählbar viele Werte annehmen kann, heißt “diskrete Zufallsvariable”. Eine Zufallsvariable, die kontinuierliche Werte annehmen kann, heißt “kontinuierliche Zufallsvariable”.

Zufallsvorgang:

Bevor dieser Vorgang durchgeführt wird, ist es ungewiss, welches Ergebnis tatsächlich eintreten wird (siehe Zufallsvariable -> Durchführung eines Versuchs). Dieses Ergebnis wird mit einer bestimmten Wahrscheinlichkeit eintreffen.

Zuverlässigkeitsuntersuchungen:

Zum Thema Zuverlässigkeitsuntersuchung (Lebensdauer-) siehe Weibullverteilung!

Literaturstellen:                (Zurück...)

Arens, Hettlic, Karpfinger, Kockelkorn, Lichtenegger, Stachel, Mathematik, SpringerSpektrum
Backhaus, Erichson, Plinke, Weiber, Multivariate Analysenmethoden, Springer Verlag
Borg, Groenen, Mair, Multidimensionale Skalierung, Rainer Hampp Verlag
Bortz, Linert, Boehnke, Verteilungsfreie Methoden in der Statistik, Springer Verlag
Bühner, Markus, Einführung in Test- und Fragebogenkonstruktion, PEARSON Studium
Burkschat, Cramer, Kamps, Beschreibende Statistik, Grundlegende Methoden, Springer-Verlag
E. Cramer, K. Cramer, Kamps, Zuckschwerdt, Beschreibende Statistik, Interaktive Grafiken, Springer-Verlag
DIN 55 350, Begriffe der Qualitätssicherung und Statistik
Eckey, Kosfeld, Rengers, Multivariate Statistik, Gabler
Günter Faes, SPC - Statistische Prozesskontrolle, BoD
Günter Faes, Einführung in R, BoD
Ludwig Fahrmeir, Künstler, Pigeot, Tutz, Statistik, Springer-Verlag
Ludwig Fahrmeir, Thomas Kneib, Stefan Lang, Regression, Springer Verlag
W. Funk, V. Dammann, G. Donnevert, Qualitätssicherung in der Analytischen Chemie, VCH
 G. W. Gottschalk, Auswertung quantitativer Analysenergebnisse,Analytiker Taschenbuch Band 1, Springer-Verlag
Handl, Andreas, Multivariate Analysemethoden, Springer
Kreis, Neuhaus, Einführung in die Zeitreihenanalyse, Springer
Kronthaler, Franz, Statistik angewandt, Springer Spektrum
Kronthaler, Franz, Statistik angewandt (mit dem R-Commander), Springer Spektrum
Ligges, Uwe,  Programmieren mit R, Springer-Verlag
Markus Oestreich, Oliver Romberg, Keine Panik vor Statistik, Vieweg + Teubner
Moosbrugger, Kelava, Testtheorie und Fragebogenkonstruktion, Springer
Montgomery, Douglas C. , Statistical Quality Control, Wiley
Helmut Pruscha, Statistische Methodenbuch, Springer
Rinne, Mittag, Prozeßfähigkeitsmessung für die industrielle Praxis, Hanser
Riedwyl, Ambühl, Statistische Auswertungen mit Regressionsprogrammen, Oldenbourg
Deborah Rumsey, Übungsbuch Statistik für Dummies, Wiley
Sachs, Angewandte Statistik, Springer-Verlag
Sachs, Hedderich, Angewandte Statistik, Springer-Verlag
Schlittgen, Rainer,  Das Statistiklabor, Springer-Verlag
Schumacher, Schulgen, Methodik klinischer Studien, Springer Verkag
Storm, Regina, Wahrscheinlichkeitsrechnung, mathematische Statistik und statistische Qualitätskontrolle, HANSER
Timischl, Wolfgang, Qualitätssicherung, Hanser
Thomas, Weir, Hass, Analysis 1 & Analysis 2, Pearson
Toutenburg, Heumann, Induktive Statistik, Springer
Guido Walz (Hg.), Lexikon der Statistik, Spektrum Akademischer Verlag
Daniel Wolschläger, Grundlagen der Datenanalyse mit R, Springer Spektrum
Zöfel, Statistik verstehen, Addison-Wesley
 

Wenn Sie möchten, können Sie Ihre Literatur direkt über diesen Link bei Amazon beschaffen!

Ihre Bestellung trägt zum Erhalt und zur Weiterentwicklung dieser Seiten bei! Danke!

Hat der Inhalt Ihnen weitergeholfen und Sie möchten diese Seiten unterstützen?